Laplaceova transformace

1.1

Příklady výpočtu přímé Laplaceovy transformace

Uvedeme základní vlastnosti přímé Laplaceovy transformace, které využíváme při řešení typických příkladů při použití vztahu (1). Jako první příklad si uvedeme odvození obrazu exponenciální funkce,

f (t) = e^{- a t}

, kde

0 < a < 1 .

F (p) = \int_{0}^{\infty} e^{- a t} e^{- p t} d t = \int_{0}^{\infty} e^{- (p + a) t} d t

Integrál exponenciály je tatáž exponenciála dělená exponetem (p+a) s dosazením integračních mezí.

F (p) = - \frac{1}{p + a} {[e^{- (p + a) t}]}_{0}^{\infty} = - \frac{1}{p + a} ⌈0 - 1⌉ = \frac{1}{p + a}

(3)

Obraz zapisujeme ve tvaru

F (p) ≜ \frac{1}{p + a}

Video 1. Definice Laplaceovy transformace – video

Jako druhý příklad uvedeme obraz jednotkového skoku

f (t) = 1 (t)

. Časový průběh jednotkového skoku je znázorněný na obrázku 2.

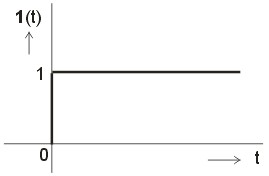
Obr. 2. Časový průběh funkce jednotkový skok

Obraz jednotkového skoku odvodíme zjednodušeně ze vztahu pro exponenciálu

f (t) = e^{- a t}

pro hodnotu koeficientu

a = 0 .

Tedy

f (t) = 1 (t)

. Obraz Jednotkového skoku odvodíme ze vztahu (3) pro

a = 0 .

F (p) ≜ \frac{1}{p}

Pro odvození obrazu funkcí

f (t) = \sin ω t

f (t) = \cos ω t

použijeme Eulerovy vztahy:

\sin ω t = \frac{e^{j ω t} - e^{- j ω t}}{2 j}

(4)

\cos ω t = \frac{e^{j ω t} + e^{- j ω t}}{2}

(5)

Naznačíme odvození obrazu funkce

f (t) = \cos ω t

. Jedná se o součet dvou exponenciál. K odvození použijeme vztah (3) pro obraz exponenciály:

F (p) = \frac{1}{2} [\frac{1}{p + j ω} + \frac{1}{p - j ω}] = \frac{1}{2} \frac{2 p}{p^{2} - j^{2} ω^{2}} = \frac{p}{p^{2} + ω^{2}} .

Obraz funkce

f (t) = \sin ω t

se odvozuje analogicky z Eulerova vztahu (5). Odvozením získáme obraz

F (p) ≜ \frac{ω}{p^{2} + ω^{2}}

Video 2. Laplaceova transformace funkcí sinus a cosinus – video

Násobení funkce exponenciálou

Definice

Nechť je

a

libovolná konstanta a nechť funkce

f (t)

, definovaná na intervalu

0 \leq t < \infty

, má obraz

F (p)

. Potom násobení funkce

f (t)

exponenciální funkcí s exponentem

a

znamená posuv v obraze

F (p)

o konstantu

a

, tedy

L \{f (t) \cdot e^{a t}\} = F (p - a)

.(6)

V tabulce 1 jsou uvedeny příklady násobení funkce exponenciálou pro funkce

f (t) = t \cdot e^{- a t}

, dále pro

f (t) = e^{- a t} \sin ω t

a pro

f (t) = e^{- a t} \cos ω t

. Uvedené funkce mají obraz posunutý o konstantu

a

V tabulce 1 je uvedený slovník základních časových funkcí a jejich Laplaceových obrazů.

Tabulka 1. Slovník funkcí a obrazů LT

Funkce	Název funkce	Obraz
$δ (t)$	dirakův puls	1
$1 (t)$	jednotkový skok	$\frac{1}{p}$
$e^{- a t}$	reálná exponenciála	$\frac{1}{p + a}$
$t$	lineární funkce	$\frac{1}{p^{2}}$
$\sin ω t$	funkce sinus	$\frac{ω}{p^{2} {+ ω}^{2}}$
$\cos ω t$	funkce cosinus	$\frac{p}{p^{2} {+ ω}^{2}}$
$t e^{- a t}$	násobení lineární funkce exponenciálou	$\frac{1}{{(p + a)}^{2}}$
$e^{- a t} \sin ω t$	násobení sinu exponenciálou	$\frac{p - a}{({p + a)}^{2} {+ ω}^{2}}$
$e^{- a t} \cos ω t$	násobení cosinu exponenciálou	$\frac{ω}{{(p + a)}^{2} {+ ω}^{2}}$

Ještě než začneme počítat příklady na Laplaceovu transformaci, uvedeme důležité vztahy mezi časovými vzory a jejich obrazy. Jedná se o linearitu mezi časovou a obrazovou funkcí, obraz konvoluce a obrazy derivace a integrálu. Tyto vztahy jsou sumarizovány v tabulce 2.

Tabulka 2. Důležité funkce Laplaceovy transformace

Předmět LT	Obraz LT	Popis funkce
$a f_{1} (t) + b f_{2} (t)$	$a F_{1} (p) + b F_{2} (p)$	Linearita platí mezi časovou i obrazovou částí.
$f (t) * h (t)$	$F (p) \cdot H (p)$	Konvoluci v časové oblasti odpovídá součin v obrazové oblasti.
$f' (t)$	$p F (p) - f (0)$	Obraz první derivace, $f (0)$ je počáteční podmínka v čase $t = 0$ .
$f'' (t)$	$p^{2} F (p) - p f (0) - f' (0)$	Obraz druhé derivace $f (0) j e p o č . p o d m í n k a a f' (0)$ je derivace počáteční podmínky.
$\int f (t) d t$	$\frac{1}{p} F (p)$	Obraz integrálu.

25 hodin

1.1.1

Příklady na přímou Laplaceovu transformaci

Na několika příkladech si procvičíme vztahy Laplaceovy transformace uvedené v tabulce 1.

Příklad

Vytvořte obraz v Laplaceově transformaci následující časové funkce, která je kombinací konstanty a exponenciálních funkcí.

f (t) = 2 + {3 e}^{- t} - 4 e^{- 2 t}

Zobrazit řešení

Řešení

Obraz funkce je

F (p) = \frac{2}{p} + \frac{3}{p + 1} - \frac{4}{p + 2}

Při odvození byla použita pravidla: linearita, obraz exponenciálních funkcí a vztah pro jednotkový skok

1 ≜ \frac{1}{p}

Příklad

Vytvořte obraz v Laplaceově transformaci následující časové funkce, která je kombinací exponenciály a sinusovky.

f (t) = 2 e^{- 2 t} + 0,5 \cdot s i n (4 t)

Zobrazit řešení

Řešení

Obraz funkce je

F (p) = \frac{2}{p + 2} + \frac{0,5 \cdot 4}{p^{2} + 16} = \frac{2}{p + 2} + \frac{2}{p^{2} + 16}

Při odvození byla použita pravidla: linearita, obraz exponenciály a vztah

\sin (ω t) ≜ \frac{ω}{p^{2} + ω^{2}}

pro

ω = 4

Příklad

Vytvořte obraz v Laplaceově transformaci následující časové funkce.

f (t) = e^{- 3 t} - 2 t

Zobrazit řešení

Řešení

Obraz funkce je:

F (p) = \frac{1}{p + 3} - \frac{2}{p^{2}}

Při odvození byla použita pravidla: linearita, obraz exponenciály a vztah pro obraz lineární funkce

t ≜ \frac{1}{p^{2}}

Příklad

Vytvořte obraz v Laplaceově transformaci následující časové funkce, která je kombinací sinu a cosinu.

f (t) = 2 \cdot \sin (2 t) - 3 \cdot \cos (2 t)

Zobrazit řešení

Řešení

Obraz funkce je:

F (p) = \frac{2 \cdot 2}{p^{2} + 4} - \frac{3 \cdot p}{p^{2} + 4} = \frac{4 + 3 p}{p^{2} + 4}

Při odvození byla použita pravidla: linearita, a vztahy pro obraz sinu a cosinu, pro

ω = 2

V další části této kapitoly si ukážeme příklad na systém popsaný diferenciální rovnicí. Základem je diferenciální rovnice prvního řádu popsaná rovnicí

f^{'} (t) = p L \{f (t)\} - f (0)

, kde

f (0)

je počáteční podmínka v čase

t = 0

. Druhou derivaci odvodíme ze vztahu

f^{''} (t) = p L \{f' (t)\}

, do této rovnice dosadíme vztah pro první derivaci

f' (t)

a obdržíme výraz

f^{''} (t) = p^{2} L \{f (t)\} - p f (0) - f' (0)

Poznámka

Někteří autoři uvádějí počáteční podmínky

f (0 +)

f' (0 +)

a vyjadřují tím, že se čas blíží k nule zprava. V textu jsou uvažovány hodnoty počátečních podmínek v čase

t = 0 .

Obrazy diferenciálních rovnic jsou znázorněné v tabulce 2.

Příklad

Uvažujme, že spojitý systém je popsaný diferenciální rovnicí

y^{''} (t) + 5 y^{'} (t) + 6 y (t) = 2 x (t)

Proměnná

y (t)

představuje výstup systému a proměnná

x (t)

je vstup, respektive buzení systému. Naším úkolem je nalézt přenosovou funkci tohoto systému, je to poměr obrazu výstupu k obrazu vstupu.

Zobrazit řešení

Řešení

Nejprve určíme obraz diferenciální rovnice druhého řádu v Laplaceově transformaci. Použijeme vztahy uvedené v tabulce 2.

p^{2} Y (p) - p f (0) - f^{'} (0) + 5 [p Y (p) - f (0)] + 6 Y (p) = 2 X (p)

Pokud položíme počáteční podmínky

f (0) = 0

f^{'} (0) = 0

, potom bude mít obraz diferenciální rovnice druhého řádu tvar:

p^{2} Y (p) + 5 p Y (p) + 6 Y (p) = 2 X (p)

Obraz diferenciální rovnice upravíme:

Y (p) [p^{2} + 5 p + 6] = 2 X (p)

Přenosová funkce

H (p)

je dána poměrem obrazu výstupu

Y (p)

a obrazu vstupu

X (p) .

H (p) = \frac{Y (p)}{X (p)} = \frac{2}{p^{2} + 5 p + 6}

Vstup

X (p)

můžeme budit jednotkovým skokem, funkcí sinus apod. V našem případě budeme systém budit Diracovým impulsem. Obraz Diracova impulsu je X(p) = 1. viz. Tabulka 1. Impulsní odezvu určíme tedy z obrazu přenosové funkce zpětnou Laplaceovou transformací.

y (t) = L^{- 1} \{Y (p\} = L^{- 1} \{\frac{2}{p^{2} + 5 p + 6}\}

Výpočet funkce impulsní odezvy

h (t)

ukážeme v kapitole o zpětné Laplaceově transformaci.

Neřešené příklady na přímou Laplaceovu transformaci

Příklad

Převeďte

časovou funkci

f (t) = e^{- 3 t} (1 - 2 s i n 3 t)

do obrazu

F (p)

Zobrazit řešení

Řešení

F (p) = \frac{1}{p + 3} - \frac{6}{{(p + 3)}^{2} + 9}

Příklad

Převeďte

časovou funkci

f (t) = 5 t + 1

do obrazu

F (p)

Zobrazit řešení

Řešení

F (p) = \frac{5}{p^{2}} + \frac{1}{p}

Příklad

Převeďte

časovou funkci

f (t) = 2 \sin t + 3 \cos t

do obrazu

F (p)

Zobrazit řešení

Řešení

F (p) = \frac{2 - 3 p}{p^{2} + 1}

Příklad

Převeďte

časovou funkci

f (t) = e^{- 3 t} \sin 2 t

do obrazu

F (p)

Zobrazit řešení

Řešení

F (p) = \frac{2}{{(p + 3)}^{2 +} + 4}

Příklad

Převeďte

časovou funkci do obrazu LT

f (t) = e^{- 2 t} \sin 3 t

Zobrazit řešení

Řešení

F (p) = \frac{3}{{(p + 2)}^{2 +} + 9}

Příklad

Převeďte

časovou funkci

f (t) = (2 t - 1) e^{- t}

do obrazu

F (p)

Zobrazit řešení

Řešení

F (p) = \frac{2}{{(p + 1)}^{2}} - \frac{1}{p + 1}

Příklad

Převeďte

časovou funkci

f (t) = {4 e}^{- t} + 2 e^{- 3 t} + \sin 2 t

do obrazu

F (p)

Zobrazit řešení

Řešení

F (p) = \frac{4}{p + 1} + \frac{2}{p + 3} + \frac{2}{p^{2} + 4}

Příklad

Určete přenosovou funkci

H (p)

k diferenciální rovnici při nulových počátečních podmínkách

y^{''} + 2 y^{'} + y = x^{'} + 2 x

Zobrazit řešení

Řešení

H (p) = \frac{p + 2}{p^{2} + 2 p + 1}

30 hodin

1.1.2

Použití Laplaceovy transformace v elektrických obvodech

Návrh a analýza elektrických obvodů obsahujících rezistory, kapacitory a induktory vedou na diferenciální rovnice. Ty je možné transformovat Laplaceovou transformací na rovnice algebraické. Jiný způsob je vyjádření obvodových rovnic pomocí Laplaceových operátorů. Základní obvodové prvky, jejich časové funkce a obrazové operátory jsou znázorněny na obrázku 3. Operátory prvků jsou uvedeny také v tabulce 3.

Obr. 3. Obvodové prvky a) rezistor b) induktor c) kapacitor

Tabulka 3. Tabulka popisu funkcí obvodových prvků v LT

Obvodový prvek	Časové funkce	Obrazy časových funkcí
rezistor	$u_{R} (t) = R \cdot i_{R} (t)$ $i_{R} (t) = \frac{u_{R} (t)}{R}$	$U_{R} (p) = R \cdot I_{R} (p)$ $I_{R} (p) = \frac{U_{R} (p)}{R}$
induktor	$u_{L} (t) = L \frac{d i_{L} (t)}{d t}$ $i_{L} (t) = \frac{1}{L} \int_{0}^{t} u_{L} (τ) d τ$	$U_{L} (p) = p L I (p) - L$ (0) $I (p) = \frac{1}{p L} U_{L} (p) + \frac{i_{L} (0)}{p}$
kapacitor	$u_{C} (t) = \frac{1}{C} \int_{0}^{t} i_{C} (τ) d τ$ $i_{C} (t) = C \frac{d u_{C} (t)}{d t}$	$U_{C} (p) = \frac{1}{p C} I_{C} (p) + \frac{u_{C} (0)}{p}$ $I_{C} (p) = C U_{C} (p) - C u_{C} (0)$

Jako příklad použijeme jednoduchý RC článek podle obrázku 4.

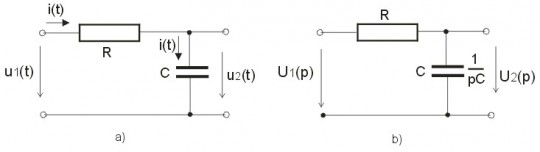
Obr. 4. RC článek a) popis v časové oblasti b) popis v operátorovém tvaru

Příklad

Pro RC článek na obrázku 4 sestavte:

diferenciální rovnici,

přenosovou funkci v operátorovém tvaru z obvodových prvků,

impulsní odezvu.

Zobrazit řešení

Řešení

Diferenciální rovnici odvodíme z rovnice pro uzel
$\frac{u_{2} (t) - u_{1} (t)}{R} + C \frac{d u_{2} (t)}{d t} = 0$
Rovnici dále upravíme
$C \frac{d u_{2} (t)}{d t} + \frac{u_{2} (t)}{R} = \frac{u_{1} (t)}{R}$
Celou rovnici vynásobíme rezistorem $R$
$R C \frac{d u_{2} (t)}{d t} + u_{2} (t) = u_{1} (t) .$
Převedeme diferenciální rovnici do operátorového tvaru a získáme přenosovou funkci
$R C p U_{2} (p) + U_{2} (p) = U_{1} (p)$ .
Počáteční napětí na kapacitoru uvažujeme $u_{2} (t) = 0$ .

Přenosovou funkci určíme pomocí obrazů obvodových prvků z tabulky 3.
$H (p) = \frac{U_{2} (p)}{U_{1} (p)} = \frac{\frac{1}{p C}}{R + \frac{1}{p C}} = \frac{1}{R C p + 1} = \frac{\frac{1}{R C}}{p + \frac{1}{R C}} .$
Pól přenosové funkce (kořen jmenovatele) je $p = - \frac{1}{R C}$ .

Impulsní odezvu integračního RC článku můžeme určit přímo ze slovníku v tabulce 1 pro vztah
$e^{- a t} ≜ \frac{1}{p + a}$ .
Impulsní odezvu určíme z přenosové funkce, při buzení Diracovým pulsem, bude
$h (t) = \frac{1}{R C} e^{\frac{- t}{R C}}$ .

Uvedeme ještě jeden příklad na určení přenosové funkce elektrického obvodu. Obvod RLC je uvedený na obrázku 5 s uvedením obrazů obvodových prvků.

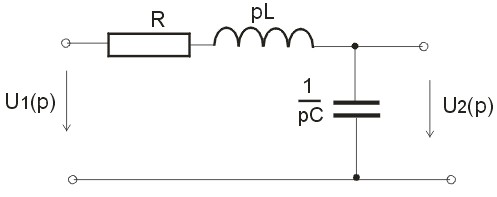
Obr. 5. Schéma obvodu RLC

Obraz výstupní funkce

U_{2} (p)

vyjádřený pomocí obrazů obvodových prvků je

U_{2} (p) = \frac{\frac{1}{p C}}{\frac{1}{p C} + p L + R} U_{1} (p) = \frac{1}{L C p^{2} + R C p + 1} U_{1} (p)

Přenosová funkce

H (p)

bude po úpravě při nulovém počátečním napětí na kapacitoru a nulovém počátečním proudu induktorem

H (p) = \frac{U_{2} (p)}{U_{1} (p)} = \frac{\frac{1}{L C}}{p^{2} + \frac{R}{L} p + \frac{1}{L C}}

20 hodin

1.1.3

Věta o posunutí (translaci).

Definice

Jestliže funkce

f (t)

má obraz

F (p)

f (t) ≜ F (p)

, potom posuneme-li funkci

f (t)

o čas

T_{D}

doprava

f (t - T_{D}) \cdot 1 (t - T_{D})

je obraz posunuté funkce násobený exponenciálou

e^{- t T_{D}}

, tedy

f (t - T_{D}) \cdot 1 (t - T_{D}) ≜ e^{- p T_{D}} \cdot F (p)

pro

T_{D} > 0

(7)

Na příkladech ukážeme výpočet obrazu funkcí popsaného typu. Připomeňme, že stále předpokládáme, že uvažované obrazy jsou deﬁnovány pouze pro nezápornou hodnotu argumentu.

Příklad

Nalezněte Laplaceův obraz funkce

f (t) = 2 \cdot t

znázorněné na obrázku 6 a jejího posunutí o

T_{D} = 3

sekundy vpravo.

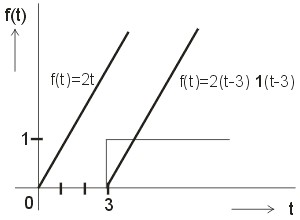
Obr. 6. Znázornění lineární funkce a jejího posunutí

Zobrazit řešení

Řešení

Obraz funkce

2 t \cdot 1 (t) ≜ \frac{2}{p^{2}}

. Jestliže funkci

f (t)

posuneme o

T_{D} = 3

sekundy, dostaneme

f (t - 3) \cdot 1 (t - 3) = 2 (t - 3) \cdot 1 (t - 3)

. Obraz posunuté funkce je

2 (t - 3) \cdot 1 (t - 3) ≜ \frac{2}{p^{2}} e^{- 3 p}

Příklad

Nyní ukážeme demonstraci věty o posunutí na vytvoření obrazu impulsu podle obrázku 7.

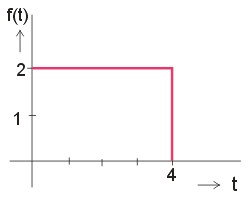
Obr. 7. Impuls délky 4 sekundy

Zobrazit řešení

Řešení

Puls vytvoříme z funkce jednotkového skoku výšky 2, od kterého odečteme v časovém okamžiku

t = 4

skok posunutý o 4 sekundy doprava, jak je znázorněno na obrázku 6. Funkci impulsu označíme

u (t)

u (t) = 2 \cdot 1 (t) - 2 \cdot 1 (t - 4) ≜ \frac{2}{p} - \frac{2}{p} e^{- 4 p} = \frac{2}{p} (1 - e^{- 4 p})

15 hodin