1.3
Goniometrický a exponenciální tvar komplexního čísla
Na obrázku 2 je vyznačený úhel
, který svírá modul
s reálnou osou. Poměr úsečky
a modulu (přepony)
je
.
Poměr imaginární složky
a modulu
je
.
Na jednotkové kružnici se dají dobře znázornit jednotlivé goniometrické funkce. Na obrázku 3 je znázorněna jednotková kružnice s vyznačením čtyř kvadrantů.
+
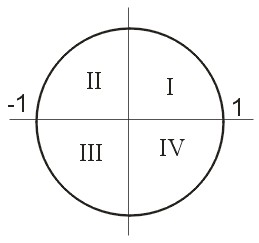
Obr. 3. Jednotková kružnice s vyznačením kvadrantů
Na obrázku 4 je znázorněna jednotková kružnice s vyznačením úhlu
. Na reálné ose je vyznačená funkce
a na imaginární ose je vyznačená funkce
.
+
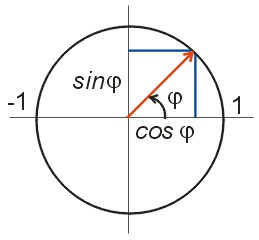
Obr. 4. Jednotková kružnice s vyznačením goniometrických funkcí
Definice
Z předchozích vztahů můžeme definovat goniometrický tvar komplexního čísla. Nechť je komplexní číslo
prvkem množiny komplexních čísel
, tedy
, potom vztah
(5)
označujeme jako goniometrický tvar komplexního čísla.
Použijeme-li Eulerův vztah pro vyjádření exponenciální funkce s komplexním exponentem. Exponenciální funkce je vyjádřena ve složkovém tvaru:
(6)
Potom získáme tzv. exponenciální tvar komplexního čísla
:
(7)
Reálné číslo
nazýváme argumentem daného komplexního čísla
. Přitom je třeba si uvědomit, že reálné číslo
není určeno jednoznačně. Jednotlivé hodnoty argumentu daného komplexního čísla se vzájemně liší o celistvé násobky
. Hodnotu úhlu
z intervalu
nazveme hlavní hodnotou argumentu komplexního čísla
. Množinu všech argumentů čísla
označujeme
.
Poznámka
V definici hlavní hodnoty argumentu nepanuje všeobecná shoda, a tak místo v intervalu
se
někdy uvažuje v intervalu
.
Komplexní čísla - video