Komplexní čísla v elektrotechnice

2.2

Kombinace obvodových prvků

V této kapitole uvedeme příklady, ve kterých budou kombinovány základní obvodové prvky – rezistory, kapacitory a induktory do složitějších obvodových celků. V další části textu budeme analyzovat kombinace základních dvojpólů. Jako první uvedeme sériovou kombinaci rezistoru a induktoru, která může představovat odpor vinutí induktoru. Obvod je buzen fázorem napětí. Z obrázku 8 je patrné schéma zapojení a také fázorový diagram.

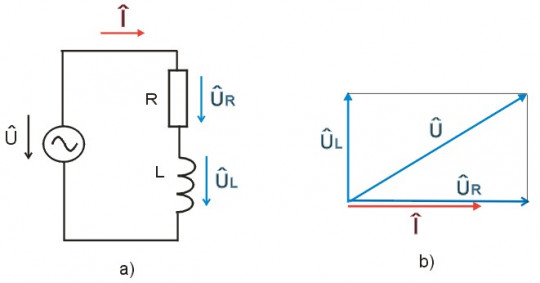
Obr. 8. a) Schéma RL sériového obvodu, b) fázorový diagram

Příklad

Zadání parametrů obvodu:

\hat{U}

= 30 V,

f

= 50 Hz,

R

= 200 Ω,

L

= 0,63 H. Vypočtěte impedanci obvodu a fázor proudu.

Zobrazit řešení

Skrýt řešení

Řešení

Impedance induktoru je

{\hat{Z}}_{L} = j ω L = j 2 π f L = j 2 π \cdot 50 s^{- 1} \cdot 0,63 H = j 314 s^{- 1} \cdot 0,63 H \approx j 200 Ω .

Celková impedance obvodu ve složkovém tvaru je

{\hat{Z}}_{R L} = R + j ω L = 200 + 200 j

. Impedance v exponenciálním tvaru je

{\hat{Z}}_{R L} = |Z| e^{j π / 4} = 283 e^{j π / 4} .

Fázor proudu dodávaný zdrojem

\hat{U}

\hat{I} = \frac{\hat{U}}{{\hat{Z}}_{R L}} = \frac{30}{283} e^{- j \frac{π}{4}}

Jako další příklad elektrického obvodu řešeného aplikací komplexních čísel bude paralelní kombinace rezistoru a kapacitoru, uvedená na obrázku 9. Je zde znázorněn obvod a fázorový diagram.

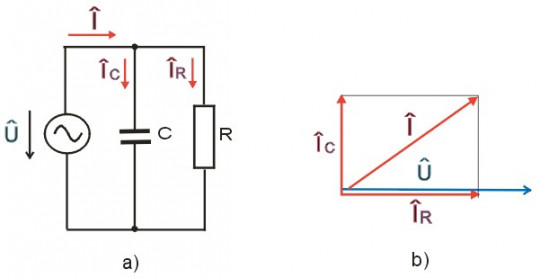
9 a) Schéma RC paralelního obvodu, b) fázorový diagram

Paralelní kombinace rezistoru a kapacitoru v přiblížení představuje svodový odpor kapacitoru.

Příklad

Zadání parametrů obvodu:

\hat{U}

= 100 V,

f

= 50 Hz,

R

= 1000 Ω,

C

=3,183 µF. Vypočtěte impedanci obvodu a fázor proudu.

Zobrazit řešení

Skrýt řešení

Řešení

Impedance kapacitoru je

{\hat{Z}}_{C} = \frac{1}{j ω C} = - \frac{j}{ω C} = - \frac{j}{314 \cdot 3,183 \cdot 10^{- 6}} = - 1000 j

. Impedance paralelní kombinace je

{\hat{Z}}_{R C} = \frac{R \cdot {\hat{Z}}_{C}}{R + {\hat{Z}}_{C}} = \frac{1000 \cdot (- 1000 j)}{1000 - 1000 j} = \frac{- 1000 j}{(1 - j)} = \frac{- 1000 j (1 + j)}{(1 - j) \cdot (1 + j)} = \frac{1000 - 1000 j}{2} = 500 - 500 j

Ω.

Impedance v exponenciálním tvaru je

{\hat{Z}}_{R C} = |Z| e^{\frac{- j π}{4}} = 707 \cdot e^{\frac{- j π}{4}}

Ω.

Proud ze zdroje je dán vztahem

\hat{I} = \frac{\hat{U}}{{\hat{Z}}_{R C}} = \frac{100}{707} \cdot e^{\frac{j π}{4}} = 0,1414 \cdot e^{\frac{j π}{4}}

Další příklady budou tvořeny kombinací kapacitoru, induktoru a rezistoru. Budeme řešit obvod uvedený na obrázku 10.

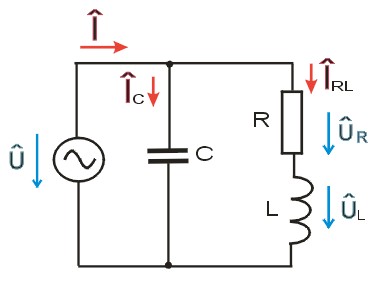
Obr. 10. Schéma elektrického obvodu C_RL

Fázorový diagram – video

Příklad

Parametry obvodu z obrázku 8 jsou následující:

\hat{U}

= 100 V,

f

= 50 Hz,

R

= 100 Ω,

C

= 10,6 µF,

L

= 0,318 H. Vypočítejte impedance obou větví obvodu a fázory proudů ve větvích. Dále vypočítejte fázory napětí na rezistoru a na induktoru.

Zobrazit řešení

Skrýt řešení

Řešení

Impedance první větve je

{\hat{Z}}_{R L} = R + j ω L = 100 + j 314 \cdot 0,318 \approx 100 + 100 j

Ω.

Impedance v druhé větvi je

{\hat{Z}}_{C} = \frac{1}{j ω C} = - \frac{j}{ω C} = - \frac{j}{314 \cdot 10,6 \cdot 10^{- 6}} = - 300 j

Ω.

Proud v první větvi je potom

{\hat{I}}_{R L} = \frac{\hat{U}}{{\hat{Z}}_{R L}} = \frac{100}{100 + 100 j} = \frac{1 - j}{(1 + j) \cdot (1 - j)} = \frac{1 - j}{2} = 0,5 - 0.5 j

Proud v druhé větvi:

{\hat{I}}_{C} = \frac{\hat{U}}{{\hat{Z}}_{C}} = \frac{100}{- 300 j} = 0,33 j

Celkový proud je dán součtem fázorů proudu

\hat{I} = {\hat{I}}_{R L} + {\hat{I}}_{C} = 0,5 - 0,5 j + 0,333 j = 0,5 - 0,167 j = 0,527 \cdot e^{- j 0,322}

Napětí na rezistoru je potom

{\hat{U}}_{R} = R \cdot {\hat{I}}_{R L}_{} = 100 \cdot \frac{1 - j}{2} = 50 \cdot (1 - j) = 50 \cdot \sqrt{2} \cdot e^{\frac{- j π}{4}}

Napětí na induktoru:

{\hat{U}}_{R L} = {\hat{Z}}_{L} \cdot {\hat{I}}_{R L}_{} = j ω L \cdot \frac{1 - j}{2} = j \frac{314 \cdot 0,318}{2} \cdot (1 - j) = 50 \cdot e^{\frac{j π}{2 \cdot}} \sqrt{2} \cdot e^{\frac{- j π}{4}} = 50 \cdot \sqrt{2} \cdot e^{\frac{j π}{4}}

Dalším příkladem elektrického obvodu je kombinace kapacitoru, induktoru a dvou rezistorů. Řešený obvod je znázorněn na obrázku 11.

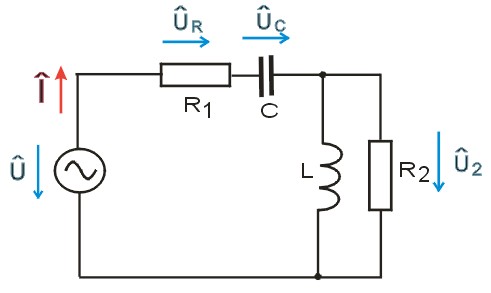
Obr. 11. Schéma elektrického obvodu

Fázorový diagram – video

Obvod budeme řešit pomocí symbolicko-komplexní metody.

Příklad

Obvod má následující parametry:

\hat{U}

= 100 V,

f

= 50 Hz,

R_{1}

= 200 Ω,

R_{2}

= 100 Ω,

C

= 15,9 µF,

L

= 0,319 H. Vypočítejte impedanci obvodu a fázor proudu.

Zobrazit řešení

Skrýt řešení

Řešení

Nejprve vypočítáme sériovou impedanci prvků

R_{1}

C

{\hat{Z}}_{R C} = R_{1} + \frac{1}{j ω C} = R_{1} + \frac{- j}{ω C} = 200 + \frac{- j}{314 \cdot 15,9 \cdot 10^{- 6}} = 200 -

200j Ω. Dále vypočítáme paralelní kombinaci

R_{2}

L

{\hat{Z}}_{R L} = \frac{R_{2} \cdot j ω L}{R_{2} + j ω L} = \frac{100 \cdot j 314 \cdot 0,319}{100 + j 314 \cdot 0,319} = \frac{100 \cdot 100 j}{100 + 100 j} = \frac{100 j}{1 + j} = \frac{100 j \cdot (1 - j)}{(1 + j) \cdot (1 - j)} = \frac{100 + 100 j}{2} = 50 + 50 j

Ω. Celkový rezistor potom bude:

{\hat{Z}}_{C} = {\hat{Z}}_{R C} + {\hat{Z}}_{R L} = 200 - 200 j + 50 + 50 j = 250 - 150 j

Ω. Vyjádření celkové impedance v exponenciálním tvaru vyjádříme jako:

{\hat{Z}}_{C} = |Z| \cdot e^{- j 0.54} = 215,5 \cdot e^{- j 0,54}

Ω. Nyní vypočítáme fázor proudu:

\hat{I} = \frac{\hat{U}}{{\hat{Z}}_{C}} = \frac{100}{251,5} \cdot e^{j 0,54}

Jako další příklad bude uveden sériový rezonanční obvod složený z rezistoru, kapacitoru a induktoru. Jeho schéma je uvedeno na obrázku 12.

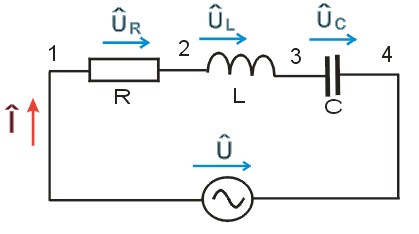
Obr. 12. Schéma rezonančního obvodu

Impedance sériového RLC obvodu je dána vztahem:

\hat{Z} = R + j ω L + \frac{1}{j ω C} = R + j (ω L - \frac{1}{ω C})

Reálná část impedance, je prezentovaná rezistorem

R

je konstantní. Naproti tomu imaginární část impedance nabývá proměnných hodnot v závislosti na velikosti složek

ω L

\frac{1}{ω C}

, které mají opačná znaménka. Hodnota imaginární část impedance sériového RLC obvodu určuje charakter obvodu. Mohou nastat tři případy

Imaginární část je $I m (\hat{Z}) < 0$ . Znamená to, že $ω L < \frac{1}{ω C}$ , kdy obvod má kapacitní charakter.

Imaginární část je $I m (\hat{Z}) > 0$ . Znamená to, že $ω L > \frac{1}{ω C}$ , kdy obvod má induktivní charakter.

Třetí případ je, kdy imaginární část impedance RLC obvodu je $I m (\hat{Z}) = 0$ . V tomto případě je impedance minimální a je rovna $\hat{Z} = R$ . V tomto případě se jedná o rezonanci.

Pokud uvažujeme napětí na jednotlivých prvcích RLC obvodu, bude napětí na rezistoru

{\hat{U}}_{R} = R \cdot \hat{I}

, napětí na induktoru

{\hat{U}}_{L} = j ω L \cdot \hat{I}

a napětí na kapacitoru

{\hat{U}}_{C} = \frac{- j}{ω C} \cdot \hat{I}

. O kapacitní charakter obvodu se jedná, je-li

{\hat{U}}_{C} > {\hat{U}}_{L}

. Indukční charakter rezonančního obvodu nastane pro

{\hat{U}}_{L} > {\hat{U}}_{C}

. Rezonance nastane pro

{\hat{U}}_{C} = {\hat{U}}_{L}

. Fázorové diagramy sériového rezonančního obvodu pro kapacitní charakter obvodu, pro induktivní charakter a pro rezonanci jsou znázorněny na obrázku 13.

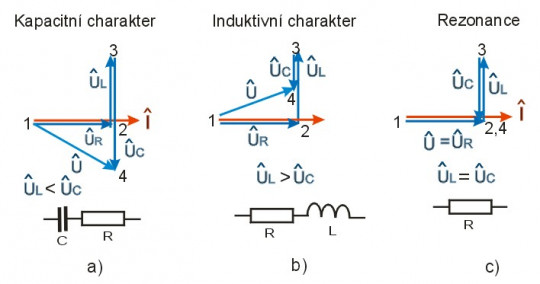
Obr. 13. Fázorové diagramy RLC obvodu a) kapacitní charakter b) induktivní charakter c) rezonance

Při rezonanci je hodnota průběhu impedance v závislosti na kmitočtu minimální. Hodnota proudu je při rezonanci naopak maximální. Průběh impedance je patrný z obrázku 14 a) a průběh proudu z obrázku 14 b).

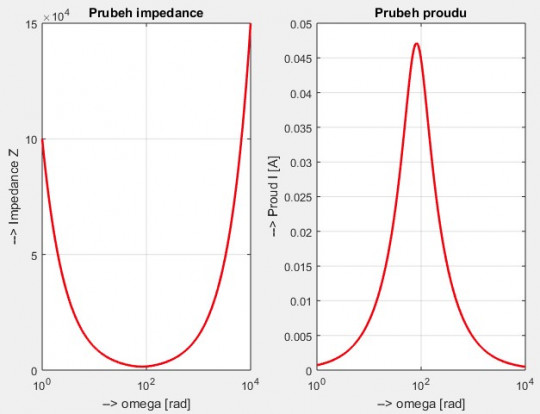
Obr. 14. a) Průběh impedance b) průběh proudu rezonančního obvodu

Oba průběhy byly kresleny v programovém prostředí Matlab pro hodnoty R=1500 Ω, L=15 H a C=10 µF. Hodnotu rezonanční frekvence vypočteme pomocí tzv. Thomsonova vzorce, který odvodíme z podmínky

ω_{r} L = \frac{1}{ω_{r} C}

, potom Thomsonův vzorec má tvar

ω_{r} = \frac{1}{\sqrt{L \cdot C}}

Rezonanční kmitočet pro dané hodnoty L a C je

ω_{r} = \frac{1}{\sqrt{L \cdot C}} = \frac{1}{\sqrt{15 \cdot 10 e - 6}} = 81,6 [r a d]

Souhrn

V první kapitole byly prezentovány základní operace s komplexními čísly. Byly uvedeny jednotlivé formáty komplexních čísel jako součtový (algebraický), goniometrický a exponenciální. V uvedených formátech byly definovány základní operace, součet a rozdíl ve složkovém tvaru, násobení a dělení v exponenciálním tvaru. Byly uvedeny převody komplexních čísel v mezi jednotlivými formáty. Byla provedena řada řešených příkladů s komplexními čísly. Druhá kapitola textu se věnovala řešení elektrických obvodů pomocí tzv. symbolicko-komplexní metody. Nejprve byl uveden popis základních obvodových prvků – rezistoru, induktoru a kapacitoru. V další části kapitoly byly analyzovány složitější elektrické obvody vzniklé kombinací základních obvodových prvků. K jednotlivým obvodům byly konstruovány fázorové diagramy. Příklady byly zakončeny sériovým rezonančním obvodem RLC a diskusí možných výsledků.