Kmitočtové charakteristiky

3.2

Kořen reálný záporný

Pro jednoduchý kořen má kořenový činitel tvar:

F (j ω) = (1 + j . \frac{ω}{ω_{0}})

Platí tedy:

F_{d B} = 20 . l o g \sqrt{1 + {(\frac{ω}{ω_{0}})}^{2}}

φ (ω) = a r c t g \frac{ω}{ω_{0}}

Průběh modulové a fázové charakteristiky je patrný z obrázku.

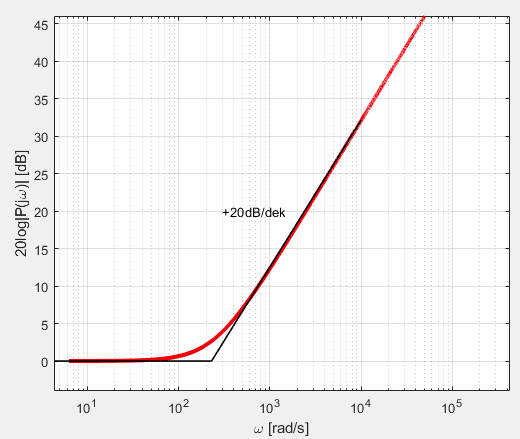
Obr. 4. Modulová charakteristika kořenového činitele záporného kořene

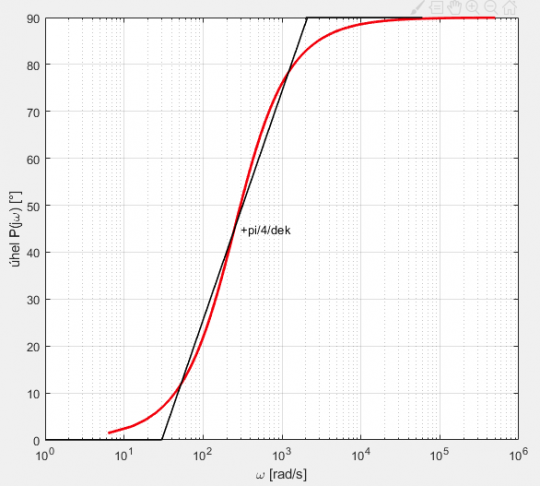
Obr. 5. Fázová charakteristika kořenového činitele záporného kořene

Pro jejich sestrojení používáme možnosti aproximace asymptotami. Postupujeme při tom následujícím způsobem:

Pro $\frac{ω}{ω_{0}} ≪ 1$ je $F (j ω) ≅ 1$ , $F_{d B} (ω) ≅ 0$ , $φ (ω) ≅ 0 .$
Modulová a fázová charakteristika se v tomto kmitočtovém pásmu blíží ose kmitočtu, která je skutečným charakteristikám asymptotou.

Pro $\frac{ω}{ω_{0}} ≫ 1$ je $F (j ω) ≅ j . \frac{ω}{ω_{0}}$ , $F_{d B} (ω) ≅ 20 . \log \frac{ω}{ω_{0}}$ , $φ (ω) ≅ \frac{π}{2}$ , což jsou charakteristiky kořenového činitele jednoduchého nulového kořene, které jsou tedy dalšími asymptotami skutečné charakteristiky.

Co se týká modulové charakteristiky, je její náhrada uvedenými asymptotami poměrně dobrou aproximací. Největší odchylka, která nastává v místě průsečíku asymptot, tj. pro

\frac{ω}{ω_{0}} = 1

, má velikost jen

∆_{F_{m a x}} = 20 . l o g \sqrt{1 + 1} ≅ 3 d B

, což pro řadu aplikací znamená zanedbatelnou hodnotu.

Náhrada fázové charakteristiky pouze dvěma asymptotami rovnoběžnými s kmitočtovou osou by byla velmi nepřesná v kmitočtovém rozsahu

10^{- 1} < \frac{ω}{ω_{0}} < 10 .

Výrazného zlepšení dosáhneme zavedením přímkového úseku, který prochází hodnotou

\frac{π}{4}

pro

\frac{ω}{ω_{0}} = 1

a má směrnici

\frac{π}{4}

na dekádu.

Největší odchylky jsou pak pro

\frac{ω}{ω_{0}} = 0,1

\frac{ω}{ω_{0}} = 10

a jejich velikost

∆_{φ_{m a x}} = a r c t g 0,1 ≅ 0,1

rad. Pokud má uvažovaný kořen násobnost n, je:

F (j ω) = {(1 + j . \frac{ω}{ω_{0}})}^{n}

F_{d B} = n . 20 . l o g \sqrt{1 + {(\frac{ω}{ω_{0}})}^{2}}

φ (ω) = n . a r c t g \frac{ω}{ω_{0}}

Průběh charakteristik je stejný, liší se jen měřítky na osách závisle proměnných. Samozřejmě také korekce asymptotických charakteristik v místě jejich lomů jsou n-krát větší.