Harmonický ustálený stav

1.1

Fázory

Z hlediska řešení obecných integrodiferenciálních obvodových rovnic daného obvodu představuje harmonický ustálený stav jejich partikulární řešení. Můžeme ho získat např. metodou odhadu, tj. předpokládáme všechny obvodové veličiny harmonické s obecnými hodnotami amplitud a fází a dosadíme do obvodových rovnic. Získáme tak soustavu goniometrických rovnic, jejich řešení je však velmi pracné a nepřehledné. Proto byla vypracována a zavedena do obvodové analýzy tzv. symbolicko-komplexní (Steinmetzova) metoda, která využívá možnosti reprezentace harmonických funkcí komplexními čísly. Vztahy mezi harmonickými funkcemi stejného kmitočtu se tak mohou převést na vztahy mezi komplexními čísly, což značně zjednodušuje všechny početní operace, s nimiž se při obvodové analýze harmonického ustáleného stavu setkáváme.

Pro plné určení harmonického průběhu stačí znalost tří parametrů, a to amplitudy, kmitočtu (nebo periody) a počáteční fáze. Pro vyjádření harmonické funkce, např. napětí, můžeme použít Eulerovy poučky ve tvaru

U_{m} . e^{j . (ω t + ψ)} = U_{m} . c o s (ω t + ψ) + j . \sin (ω t + ψ)

Odtud vyplývá, že můžeme vyjádřit harmonickou funkci pomoci komplexní funkce reálné proměnné t

U_{m} . e^{j . (ω t + ψ)} = U_{m} . e^{j . ψ} . e^{j . ω t} = U_{m} . e^{j . ω t}

ve tvaru

u (t) = U_{m} . s i n (ω t + ψ) = I m [U_{m} . e^{j . (ω t + ψ)}] = I m [U_{m} . e^{j . ψ} . e^{j . ω t}] = I m [U_{m} . e^{j . ω t}]

Tuto funkci můžeme zobrazit pro libovolný časový okamžik

t = t_{k}

v komplexní rovině jako koncový bod vektoru délky

U_{m}

, svírající s reálnou osou úhel

ω t_{k} + ψ

. S rostoucím časem se tento bod pohybuje po kružnici o poloměru

U_{m}

a uvažovaný vektor rotuje kolem počátku úhlovou rychlostí

ω

Definice

Zjednodušeně řečeno je fázor vektor, který v komplexní rovině rotuje úhlovou rychlostí

ω

Okamžité hodnoty harmonického napětí

u (t)

získáme jako jeho průměty do imaginární osy, viz obr. 4.

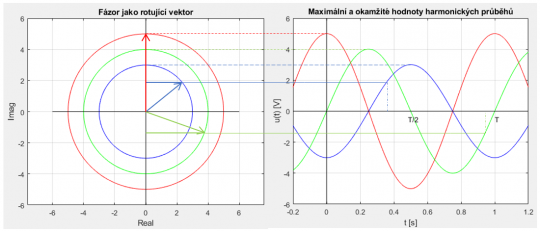
Obr. 4. Maximální a okamžité hodnoty

Video 2. Maximální a okamžité hodnoty

To také odpovídá konstrukci harmonického průběhu zmíněné v předchozí části. Rotující vektor je tedy úplným reprezentantem harmonického průběhu, protože jsou v něm obsaženy všechny tři potřebné parametry a umožňuje stanovení funkční hodnoty v libovolném okamžiku.

V harmonickém ustáleném stavu je kmitočet všech veličin obvodu stejný, takže každou z nich stačí charakterizovat pouze dvěma parametry, a to amplitudou a fází. Tyto parametry jsou však již obsaženy v samotném komplexním čísle

U = \frac{U_{m}}{\sqrt{2}} = \frac{U_{m}}{\sqrt{2}} . e^{j . ψ} = U . e^{j . ψ}

Pro rozlišení ho označujeme jako fázor v měřítku efektivních hodnot a fázor

U_{m}

nazýváme fázorem v měřítku amplitud. Časový průběh harmonické veličiny vyjádříme pomoci fázoru v měřítku efektivních hodnot vztahem

u (t) = \sqrt{2} . I m [U . e^{j . (ω t)}]

Při definici fázoru jsme vzali za základ harmonický průběh vyjádřený funkcí sinus. Stejně dobře můžeme ale použít vyjádřeni pomocí funkce kosinus.

V tomto případě má vyjádření časového průběhu pomocí fázoru tvar

u (t) = U_{m} . c o s (ω t + ψ) = R e [U_{m} . e^{j . (ω t + ψ)}] = R e [U_{m} . e^{j . ψ} . e^{j . ω t}] = R e [U_{m} . e^{j . ω t}]

Jak jsme uvedli, budeme dávat přednost vyjádření harmonických funkcí pomocí funkce sinus. Fázory budeme zapisovat velkým tučným písmem, tj.

U

I

. Při používání symbolické metody musíme mít vždy na paměti, že se jedná o jistý druh transformace, která přiřazuje reálné harmonické funkci reálné proměnné, kterou je čas, komplexní konstantu. Zpětnou transformací přiřazujeme této konstantě odpovídající časový průběh. I když se v praxi často fázory obvodových veličin označují přímo jako "napětí" a "proud", nelze je nikdy s časovými průběhy zaměňovat. Početní operace s harmonickými veličinami, s nimiž se při analýze harmonického ustáleného stavu setkáme, můžeme převést na podstatně jednodušší operace s fázory, musíme se však omezit jen na operace, při nichž se kmitočet harmonických funkcí nemění.

Součet harmonických veličin stejného kmitočtu je opět harmonická veličina téhož kmitočtu, tj.

\sum_{k = 1}^{n} U_{m k} . s i n (ω t + ψ_{k}) = U_{m} . s i n (ω t + ψ)

Vyjádříme-li všechny členy této rovnice pomocí fázorů, dostaneme

\sum_{k = 1}^{n} I m [U_{m k} . e^{j . (ω t)}] = I m [U_{m} . e^{j . ω t}]

a tedy platí

\sum_{k = 1}^{n} U_{m k} = U_{m}

Definice

Fázor součtu harmonických veličin je roven součtu fázorů jednotlivých sčítanců.

Poznámka

Kirchhoffovy zákony platí rovněž pro fázory napětí a proudů

\sum_{k = 1}^{n} U_{k} = 0

\sum_{k = 1}^{n} I_{k} = 0

Příklad:

Příklad

Vyjádřete harmonická napětí s časovými průběhy

u_{1} (t) = 40 . s i n (1000 t + 0,3)

u_{2} (t) = 30 . s i n (1000 t + 1,1)

pomocí fázorů v měřítku amplitud a efektivních hodnot.

Určete časový průběh součtového napětí

{u (t) = u}_{1} (t) + u_{2} (t)

Zobrazit řešení

Skrýt řešení

Řešení

U_{m 1} = 40 . e^{j . 0,3}

U_{m 2} = 30 . e^{j . 1,1}

Fázory v měřítku efektivních hodnot jsou:

U_{1} = \frac{U_{m 1}}{\sqrt{2}} = \frac{40 . e^{j . 0,3}}{\sqrt{2}} = 28,28 . e^{j . 0,3}

U_{2} = \frac{U_{m 2}}{\sqrt{2}} = \frac{30 . e^{j . 1,1}}{\sqrt{2}} = 21,21 . e^{j . 1,1}

U_{m 1} = 40 . (c o s 0,3 + j . s i n 0,3) = 38,21 + j . 11,82

U_{m 2} = 30 . (c o s 1,1 + j . s i n 1,1) = 13,61 + j . 26,74

U_{m} = 51,82 + j . 38, 56 = 64,59 . e^{j . 0,6397}

u (t) = 64,59 . s i n (1000 t + 0,6397)

Obr. 5. Součet dvou fázorů napětí