4.4
Karnaughovy mapy
Karnaughovy mapy představují jednoduchý grafický způsob reprezentace logických funkcí.
Definice
Každé políčko v Karnaughově mapě odpovídá jednomu součinovému termu nezávisle proměnných funkce, tedy jednomu řádku úplné pravdivostní tabulky dané funkce.
Mapa obsahuje pro n nezávisle proměnných vždy celkem 2n políček.
Políčka v Karnaughově mapě kódujeme pomocí tzv. Grayova kódu.
Definice
Grayův kód je binární kód, ve kterém se dvě po sobě následující čísla v binárním zápise navzájem liší v hodnotě pouze na jednom řádovém místě.
Zajímavost
Počet řádových míst, na kterých se navzájem liší dvě čísla zapsaná v binárním kódu, se označuje jako tzv. Hammingova vzdálenost.
V případě Grayova kódu tedy platí, že Hammingova vzdálenost dvou po sobě následujících čísel je vždy rovna právě 1.
Převod čísel 0 až 9 mezi přímým binárním kódem a Grayovým kódem obsahuje tabulka 9.
Tabulka 9. Převodní tabulka čísel 0-9 mezi přímým binárním kódem a Grayovým kódem.
Desítkové vyjádření
Přímý binární kód (jednotlivé pozice)
Grayův kód (jednotlivé pozice)
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
1
2
0
0
1
0
0
0
1
1
3
0
0
1
1
0
0
1
0
4
0
1
0
0
0
1
1
0
5
0
1
0
1
0
1
1
1
6
0
1
1
0
0
1
0
1
7
0
1
1
1
0
1
0
0
8
1
0
0
0
1
1
0
0
9
1
0
0
1
1
1
0
1
Zajímavost
Kromě Karnaughových map existují i jiné druhy map, které se navzájem liší různým způsobem číslování políček v mapě. Např. Svobodovy mapy používají ke kódování políček přímý binární kód. Z hlediska snadnosti zápisu a použití mapy pro minimalizaci logické funkce jsou však Karnaughovy mapy do počtu 6 nezávisle proměnných (64 políček v mapě) nejvýhodnější.
Pořadí přiřazení jednotlivých nezávisle proměnných oblastem v Karnaughově mapě je libovolné, nicméně stejně jako v případě pravdivostní tabulky je obvyklé přiřazení proměnné a k nejnižšímu řádovému místu binárního vyjádření indexů políček v mapě. Každá další proměnná v abecedním pořadí je následně přiřazována postupně na vyšší řádové místo.
Pro jednu nezávisle proměnnou a obsahuje mapa 21 = 2 políčka s indexy 0 a 1, jak ukazuje obrázek 15.
+
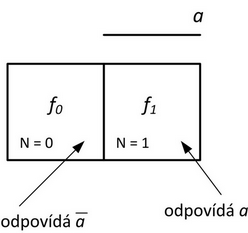
15. Karnaughova mapa pro 1 proměnnou
Obr. 15. Karnaughova mapa pro 1 proměnnou
Definice
Oblast pokrytí každou proměnnou v mapě obvykle vyznačujeme pomocí svislých a vodorovných čar po okrajích mapy.
Pro každou Karnaughovu mapu vždy platí, že přesně polovina políček v mapě leží v oblasti pokrytí danou proměnnou a druhá polovina mimo ni. V polovině mapy je vždy daná proměnná rovna logické 1 a v druhé polovině mapy je rovna logické 0.
Pro dvě nezávisle proměnné a, b obsahuje mapa 22 = 4 políčka, viz obrázek 16.
+
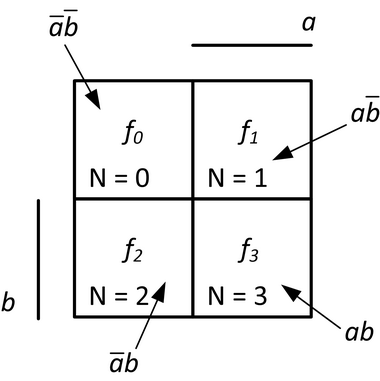
16. Karnaughova mapa pro 2 proměnné
Obr. 16. Karnaughova mapa pro 2 proměnné
Pro trojici nezávisle proměnných a, b, c má mapa již 23 = 8 políček. Zároveň se v ní již uplatní číslování políček dle Grayova kódu, jak ukazuje obrázek 17.
+
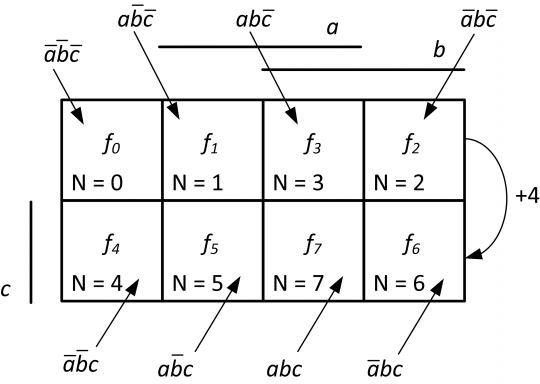
17. Karnaughova mapa pro 3 proměnné
Obr. 17. Karnaughova mapa pro 3 proměnné
Poznámka
Pro označení políček Karnaughovy mapy si lze zapamatovat jednoduchou pomůcku. Postačí si zapamatovat první čtveřici čísel v Grayově kódu: 0, 1, 3, 2. V tomto pořadí očíslujeme políčka na prvním řádku mapy zleva doprava. Druhý řádek v mapě je pak již jen posunutý o +4, tzn. 0 + 4 = 4, 1 + 4 = 5, 3 + 4 = 7 a 2 + 4 = 6.
Čtveřice nezávisle proměnných a, b, c, d, vyžaduje Karnaughovu mapu již s 24 = 16 políčky, viz obrázek 18.
+
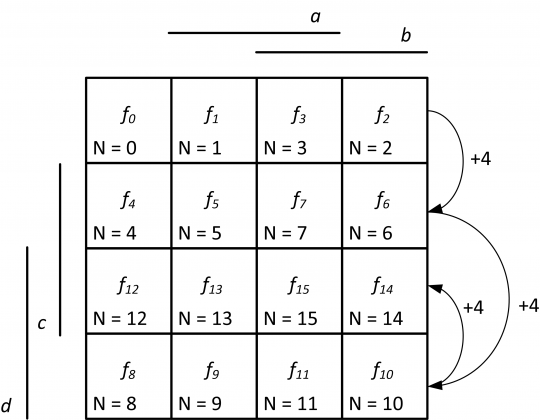
18. Karnaughova mapa pro 4 proměnné
Obr. 18. Karnaughova mapa pro 4 proměnné
Poznámka
Pro číslování políček mapy si lze opět zapamatovat jednoduchou pomůcku. První řádek zleva doprava je opět očíslován: 0, 1, 3 a 2. Druhý řádek je o +4 zvětšen. Následně poslední, čtvrtý řádek mapy, je od druhého zvětšen o +4. Jako poslední očíslujeme třetí řádek mapy opět přičtením +4 ke čtvrtému řádku.
Pro zakreslení mapy s pěti proměnnými, a, b, c, d, e potřebujeme již 25 = 32 políček, obrázek 19.
+
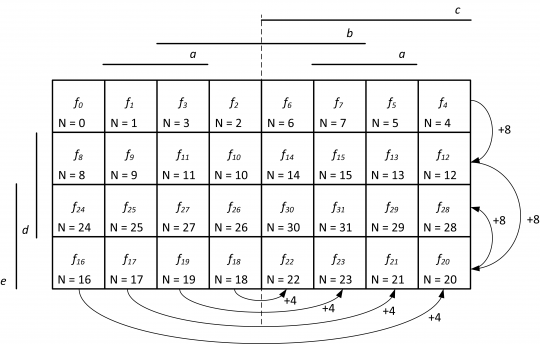
19. Karnaughova mapa pro 5 proměnných
Obr. 19. Karnaughova mapa pro 5 proměnných
Pro Karnaughovy mapy s pěti proměnnými a více se již v mapách uplatňují osy symetrie. V mapě pro 5 proměnných je jedna osa symetrie umístěná vertikálně uprostřed mapy a rozděluje ji na dvě osově symetrické části. Mapu pak pomocí této osy můžeme „složit“, což má význam při hledání tzv. sousedních políček v mapě.
Poznámka
Osu symetrie v mapě můžeme rovněž využít pro správné očíslování jejích políček. V levé polovině je opět první řádek očíslován zleva doprava: 0, 1, 3 a 2. Pravá polovina řádku je pak osově symetricky posunuta o +4 vůči levé polovině řádku, tedy opět zleva doprava: 2 + 4 = 6, 3 + 4 = 7, 1 + 4 = 5 a 0 + 4 = 4. Po doplnění číslování prvního řádku můžeme indexy políček na druhém řádku získat přičtením +8 k prvnímu řádku. Dále indexy ve čtvrtém řádku jsou opět posunuty o +8 oproti druhému řádku a konečně třetí řádek získáme přičtením +8 ke čtvrtému.
Zajímavost
V mapě pro 5 proměnných si lze povšimnout, že oblast pokrytá proměnnou a je rozdělena na dvě nesouvislé poloviny; jedna pokrývá prostřední dva sloupečky v levé polovině mapy, druhá je pak osově symetricky umístěna v prostředních dvou sloupcích v pravé polovině mapy.
Výhody
Hlavní výhodou a účelem využití Karnaughových map je minimalizace logických funkcí a převody forem funkcí navzájem (vzájemný převod forem ÚNDF, ÚNKF). Tomuto tématu se věnuje navazující text „Minimalizace logických funkcí a jejich realizace pomocí hradel“.
Nevýhody
Karnaughovy mapy a mapy obecně, kromě procesu minimalizace a převodů forem funkcí, nenabízí žádné jiné výhody. Další nevýhodou je obvykle pracnost a zdlouhavost jejich zakreslení.
Příklad
Karnaughovu mapu funkce f z příkladu v pravdivostní tabulce 7 můžeme zakreslit tak, jak ukazuje obrázek 20.
+
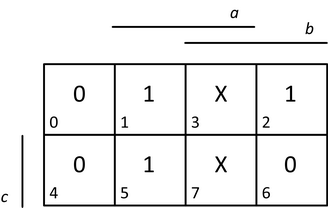
20. Karnaughova mapa pro funkci f z pravdivostní tabulky 7
Obr. 20. Karnaughova mapa pro funkci f z pravdivostní tabulky 7