2.2
Minimalizace logických funkcí pomocí Karnaughových map
Postup minimalizace logické funkce pomocí Karnaughovy mapy můžeme shrnout do několika kroků, respektive několika pravidel pomocí kterých minimální formu v mapě určíme.
Souhrn
  1. Nakreslíme Karnaughovu mapu pro daný počet nezávisle proměnných, očíslujeme její políčka v souladu s pravidly Grayova kódu a vepíšeme do mapy funkční hodnoty zadané funkce.
    1. Pro hledání MNDF do mapy vyplníme jednotkové body a neurčité stavy.
    1. Při hledání MNKF do mapy vyplníme nulové body a neurčité stavy.
  1. Postupně v mapě vytváříme smyčky (podmapy) podle těchto pravidel:
    1. můžeme spojovat pouze navzájem sousední políčka v mapě (viz předchozí kapitola),
    1. smíme spolu spojovat jen políčka se stejnými funkčními hodnotami nebo neurčitými stavy (tzn. můžeme spojit políčka s logickými 1 nebo logickými 1 a neurčitými stavy, stejně tak můžeme logické 0 spojit jen s jinými logickými 0 nebo s neurčitými stavy),
    1. počet políček ve vytvořené smyčce (podmapě) musí odpovídat mocnině čísla 2 – tzn. lze vytvořit pouze podmapy o velikosti: 0, 1, 2, 4, 8, 16, 32… políček,
    1. smyčky (podmapy) vytváříme v mapě co možná největší – jen tak získáme minimální formu funkce (těmto smyčkám odpovídají prosté implikanty),
    1. výsledný počet smyček v mapě se snažíme vytvořit co nejmenší – získáme tak co nejmenší počet implikantů,
    1. smyčky se mohou v mapě libovolně překrývat – jedno políčko tedy může klidně náležet do několika smyček, pokud nám to pomůže tyto smyčky vytvořit co největší.
  1. Pomocí těchto pravidel postupujeme tak, aby:
    1. v případě MNDF formy byly všechny logické 1 v mapě zahrnuty do alespoň jedné smyčky (všechna políčka s logickými 1 musí být pokryta alespoň jednou smyčkou),
    1. pokud hledáme MNKF formu, musí být všechny logické 0 funkce zahrnuty v alespoň jedné smyčce (všechna políčka s logickými 0 musí být pokryta alespoň jednou smyčkou),
    1. neurčité stavy v obou formách mohou, ale nemusí být zahrnuty do smyček – pokud se nám dané políčko s neurčitým stavem hodí pro vytvoření větší smyčky v mapě, pokud se nám nijak nehodí, necháme neurčitý stav nepokrytý.
  1. Každou smyčku v mapě následně vyjádříme jako součinový term nezávisle proměnných, jejichž hodnoty se v rámci dané smyčky nemění (k tomu nám jako pomůcka slouží oblasti pokrytí proměnnými v mapě vyznačené pomocí svislých a vodorovných čar po okrajích mapy).
  1. Výsledné MNDF řešení získáme jako logický součet jednotlivých součinových termů vzniklých pomocí smyček z logických 1 a neurčitých stavů, MNKF řešení je pak rovno NEGACI logického součtu jednotlivých součinových termů vytvořených ze smyček logických 0 a neurčitých stavů
  1. V některých případech může existovat více rovnocenně minimálních řešení.
Zajímavost
Z definice uvedené v předchozí kapitole, že v mapě pro n proměnných existuje ke každému jejímu políčku právě n sousedních políček, vyplývá s ohledem na velikost smyček, že v případě mapy s n nezávisle proměnnými obsahuje součinový term vzniklý ze smyčky o velikosti:
  • 1 políčko – term obsahuje n proměnných,
  • 2 políčka – term obsahuje n-1 proměnných,
  • 4 políčka – term obsahuje n-2 proměnných,
  • 8 políček – term obsahuje n-3 proměnných,
  • 16 políček – term obsahuje n-4 proměnných,
  • …
Obecně označme počet nezávisle proměnných v mapě jako n a počet políček, která tvoří danou smyčku, jako p, pak součinový term vzniklý z dané smyčky bude obsahovat právě počet proměnných x, kde x můžeme vyjádřit jako:
x=n-log2⁡p .
Uvedený postup minimalizace logické funkce pomocí hledání smyček v mapě si předvedeme na několika příkladech.
Příklad
Příklad:
Nalezněte MNDF a MNKF formy funkce f čtyř nezávisle proměnných a, b, c, d zadané pomocí zkráceného seznamu stavových indexů. MNDF formu realizujte pomocí hradel NAND, MNKF formu pomocí hradel NOR.
f = 0, 2, 4, 6, 7, 8, 10, (11), (15).
Zobrazit řešení
Řešení
Řešení:
Nakreslíme Karnaughovu mapu pro 4 proměnné, očíslujeme její políčka a vyplníme hodnoty zadané funkce, jak ukazuje obrázek 6.
+
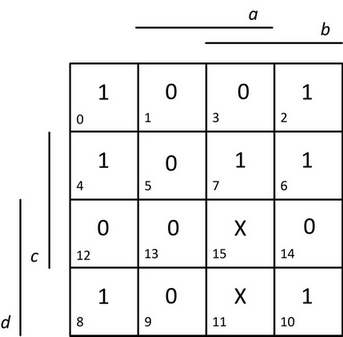
6. Karnaughova mapa zadané funkce čtyř proměnných
Obr. 6. Karnaughova mapa zadané funkce čtyř proměnných
1. Nejprve nalezneme MNDF formu funkce f a realizujeme ji pomocí hradel NAND.
V mapě nás tak budou nyní zajímat pouze políčka obsahující logické 1 a neurčité stavy. Pomocí pravidel uvedených výše nalezneme a v mapě vyznačíme příslušné smyčky, jak ukazuje obrázek 7.
+
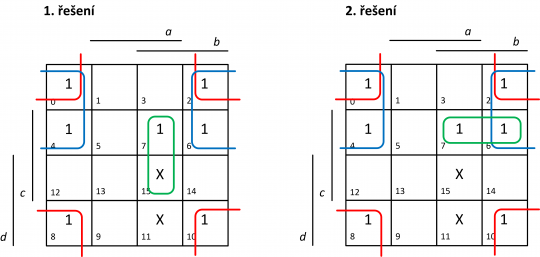
7. Dvě rovnocenně minimální řešení MNDF formy zadané funkce
Obr. 7. Dvě rovnocenně minimální řešení MNDF formy zadané funkce
Zadaný příklad má dvě rovnocenně minimální řešení, viz dále.
V mapě jsme nalezli tyto smyčky:
  • červená smyčka – je tvořena políčky 0, 2, 8 a 10, pokud mapu stočíme seshora dolů i zleva doprava, dostanou se všechny 4 rohy mapy navzájem k sobě a můžeme z nich vytvořit jednu smyčku sousedních políček,
  • modrá smyčka – políčka s indexy 0, 2, 4 a 6 jsou navzájem sousední přes okraj mapy,
  • zelená smyčka – protože z políček obsahujících logickou 1 zbývá nepokryté políčko 7, je potřeba ještě jedna smyčka k jeho pokrytí. Zde se nabízí dvě možnosti, dvě rovnocenně minimální řešení. První řešení představuje smyčka políčka 7 s políčkem 15, které obsahuje neurčitý stav. Druhé řešení je vytvořit smyčku z políčka 7 a již pokrytého políčka 6.
Políčko s indexem 11 obsahující neurčitý stav se nám nehodilo do žádné ze smyček, abychom pomocí něho vytvořili některou smyčku větší. Necháme jej tedy nepokryté.
Zapíšeme nyní součinové termy pro jednotlivé smyčky:
  • červená smyčka – a¯⋅c¯ ,
  • modrá smyčka – a¯⋅d¯ ,
  • zelená smyčka – 1. řešení: a⋅b⋅c , 2. řešení: b⋅c⋅d¯ .
Dvě řešení MNDF – fD1, fD2 – pak zapíšeme jako logické součty jednotlivých součinových termů:
fD1=a¯⋅c¯∨a¯⋅d¯∨a⋅b⋅c
fD2=a¯⋅c¯∨a¯⋅d¯∨b⋅c⋅d¯
Obě dvě řešení bychom nyní realizovali pomocí hradel NAND. MNDF formu je však nutno nejprve upravit do tvaru negovaných logických součinů. Použijeme tedy stejný postup jako v předchozím příkladu v kapitole 1.2, tedy nejprve aplikujeme zákon dvojité negace a následně zákon o negaci logického součtu. Upravíme postupně obě řešení:
fD1=a¯⋅c¯∨a¯⋅d¯∨a⋅b⋅c=a¯⋅c¯∨a¯⋅d¯∨a⋅b⋅c¯¯=a¯⋅c¯¯⋅a¯⋅d¯¯⋅a⋅b⋅c¯¯
fD2=a¯⋅c¯∨a¯⋅d¯∨b⋅c⋅d¯=a¯⋅c¯∨a¯⋅d¯∨b⋅c⋅d¯¯¯=a¯⋅c¯¯⋅a¯⋅d¯¯⋅b⋅c⋅d¯¯¯
Jejich realizaci pomocí hradel NAND pak ilustruje následující obrázek 8.
+
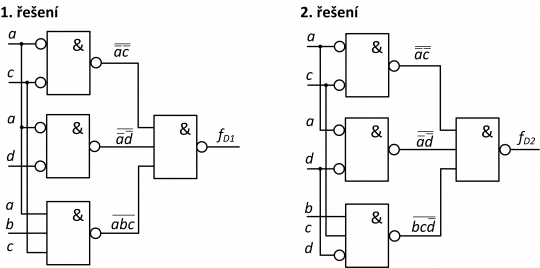
8. Realizace obou MNDF řešení funkce z příkladu pomocí hradel NAND
Obr. 8. Realizace obou MNDF řešení funkce z příkladu pomocí hradel NAND
Negace vstupních proměnných tam, kde je potřeba, jsme pro lepší přehlednost v obrázku vyznačili pouze kroužkem na vstupu hradla a nerozkreslovali jsme hradla NAND pro vytvoření negace dle obrázku 2.
2. Nyní se zaměříme na MNKF formu funkce f a její realizaci pomocí hradel NOR.
Do mapy proto vyplníme políčka s hodnotou funkce logická 0 nebo neurčitý stav. Opět pomocí pravidel pro hledání smyček v mapě nalezneme MNKF pomocí smyček přes nulové body a/nebo neurčité stavy, výsledek je zobrazen na obrázku 9.
+
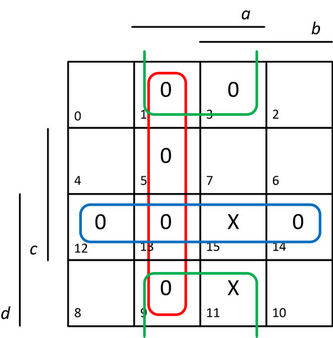
9. Vytvoření smyček v mapě zadané funkce f pro hledání MNKF formy
Obr. 9. Vytvoření smyček v mapě zadané funkce f pro hledání MNKF formy
Pro pokrytí všech nulových bodů funkce pomocí co nejmenšího počtu co největších smyček jsme potřebovali celkem 3 smyčky:
  • červená smyčka – tvořená políčky 1, 5, 9 a 13, která jsou všechna navzájem sousední,
  • modrá smyčka – složená z políček s indexy 12, 13, 14 a 15, ve které jsme využili i neurčitý stav v políčku číslo 15,
  • zelená smyčka – obsahující políčka s indexy 1, 3, 9 a 11, která vznikne po stočení mapy seshora dolů, kdy spodní hrana mapy a horní hrana mapy spolu sousedí. Ve smyčce jsme opět s výhodou použili neurčitý stav v políčku 11, políčka 1 a 9 patří do červené smyčky i zelené smyčky (smyčky se překrývají).
V případě určení MNKF formy jsme vhodně využili oba neurčité stavy. Na rozdíl od předchozí MNDF formy funkce f, je minimální řešení pro MNKF formu pouze jedno. Zapíšeme jej tedy takto:
  • červená smyčka – a⋅b¯ ,
  • modrá smyčka – c⋅d ,
  • zelená smyčka – a⋅c¯ .
Výsledná MNKF forma fK je negací logického součtu výše uvedených součinových termů. Upravíme negaci na základě zákonů o negaci logického součtu a součinu postupně v krocích:
fK=a⋅b¯∨c⋅d∨a⋅c¯¯=a⋅b¯¯⋅c⋅d¯⋅a⋅c¯¯=a¯∨b⋅c¯∨d¯⋅a¯∨c .
Pro realizaci MNKF formy dle fK zvolíme hradla NOR. Opět je ale potřeba nejprve výraz upravit do podoby negovaných logických součtů. S výhodou opět použijeme zákon dvojité negace a zákon o negaci logického součinu, získáme tak výraz:
fK=a¯∨b⋅c¯∨d¯⋅a¯∨c¯¯=a¯∨b¯∨c¯∨d¯¯∨a¯∨c¯¯
který již můžeme snadno realizovat pomocí hradel NOR, jak ukazuje obrázek 10. V něm jsme opět pro lepší přehlednost zakreslili kroužkem na vstupech hradel negace nezávisle proměnných.
+
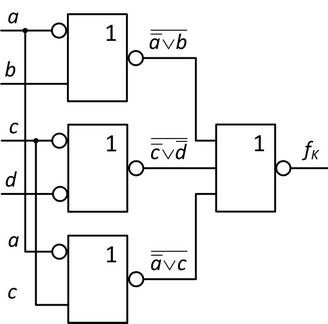
10. Realizace MNKF formy z příkladu pomocí hradel NOR
Obr. 10. Realizace MNKF formy z příkladu pomocí hradel NOR
Příklad
Příklad:
Nalezněte MNDF a MNKF formy funkce f pěti proměnných a, b, c, d, e zadané pomocí zkráceného seznamu stavových indexů. Realizujte MNDF formu pomocí hradel NAND, MNKF formu pomocí hradel NOR. Pro každou z forem stačí nalézt jedno libovolné minimální řešení (pokud existuje více rovnocenně minimálních, postačí jedno libovolné z nich). Funkce f je zadána indexy:
f = 0, (1), 2, 4, 5, (6), 9, 11, 13, 14, (15), 16, 18, 20, 22, (25), 27, 29, (30), 31.
Zobrazit řešení
Řešení
Řešení.
Jedná se o funkci pěti proměnných, nejprve nakreslíme příslušnou Karnaughovu mapu, očíslujeme její políčka a vyplníme do ní hodnoty zadané funkce f, jak ukazuje obrázek 11. Nezapomeneme na osu symetrie, která prochází vertikálně středem mapy.
+
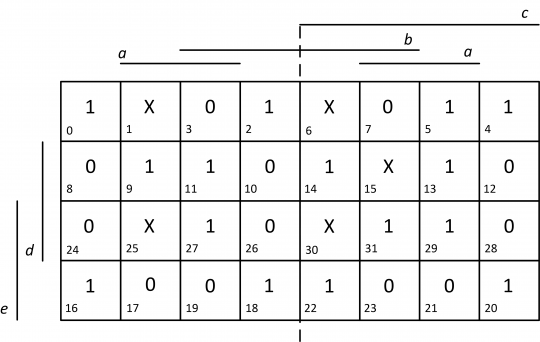
11. Vyplněná Karnaughova mapa funkce f pěti proměnných z příkladu
Obr. 11. Vyplněná Karnaughova mapa funkce f pěti proměnných z příkladu
Postup nalezení formy MNDF i formy MNKF přehledně ukazuje následující animace 1.
Animace 1. Animace řešení nalezení forem MNDF i MNKF zadané funkce f pěti proměnných
Výsledkem minimalizace jsou MNDF a MNKF formy:
fD=a¯⋅d¯∨a⋅d∨a¯⋅b⋅c∨b¯⋅d¯⋅e¯
fK=a¯⋅b¯⋅d∨a¯⋅c¯⋅d∨a⋅b⋅d¯∨a⋅d¯⋅e¯=a∨b∨d¯⋅a∨c∨d¯⋅a¯∨b¯∨d⋅a¯∨d∨e¯
V případě MNDF formy se v mapě nabízí více rovnocenně minimálních řešení (celkem 4 možná řešení) – dokážete je nalézt?
Pro realizace MNDF a MNKF forem pomocí hradel je opět potřeba upravit jejich vyjádření pomocí zákona dvojité negace a zákonů o negaci logického součtu a součinu do vhodných tvarů:
fD=a¯⋅d¯∨a⋅d∨a¯⋅b⋅c∨b¯⋅d¯⋅e¯=a¯⋅d¯¯⋅a⋅d¯⋅a¯⋅b⋅c¯⋅b¯⋅d¯⋅e¯¯¯ 
fK=a∨b∨d¯⋅a∨c∨d¯⋅a¯∨b¯∨d⋅a¯∨d∨e¯=a∨b∨d¯¯∨a∨c∨d¯¯∨a¯∨b¯∨d¯∨a¯∨d∨e¯¯¯
Realizaci MNDF formy provedeme opět pomocí hradel NAND, výsledek je uveden na obrázku 12.
+
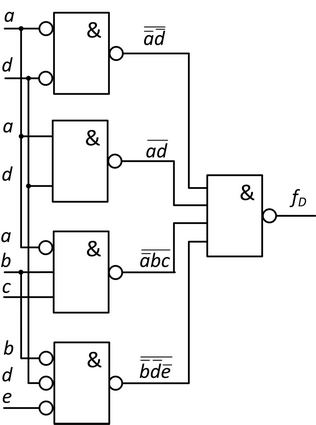
12. Realizace získané MNDF formy pomocí hradel NAND
Obr. 12. Realizace získané MNDF formy pomocí hradel NAND
A stejným způsobem pak realizujeme i MNKF formu, tu však pomocí hradel NOR, jak ukazuje obrázek 13.
+
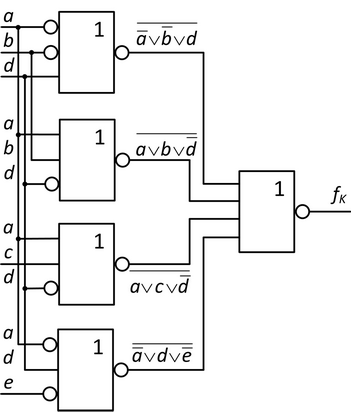
13. Realizace získané MNKF formy pomocí hradel NOR
Obr. 13. Realizace získané MNKF formy pomocí hradel NOR
Výhody
Při porovnání metod minimalizace logických funkcí pomocí algebraických úprav a pomocí Karnaughových map je zřejmé, že Karnaughovy mapy nabízí rychlý, přehledný a relativně jednouchý způsob pro hledání minimálních forem funkcí. Mapy lze navíc výhodně použit i pro převody forem funkcí, viz další kapitola.
Nevýhody
Mezi hlavní nevýhody použití Karnaughových map pro minimalizaci logických funkcí patří skutečnost, že hledání smyček v mapě je značně intuitivní záležitost, která vyžaduje dostatečné zkušenosti a představivost při hledání co nejmenšího počtu co největších smyček v mapách. Z tohoto důvodu nelze jednoduše realizovat metodu minimalizace logických funkcí prostřednictvím Karnaughových map pomocí počítačového (programátorského) řešení, např. vhodným algoritmem. Nevýhodou Karnaughových map rovněž je, že do počtu proměnných 6 nabízí ještě dostatečnou přehlednost, se zvyšujícím se počtem proměnných (7 a více) jsou mapy značně složité, nepřehledné a pracné na zakreslení.
Zajímavost
Na internetu lze nalézt množství online i offline nástrojů Karnaughových map pro minimalizaci logických funkcí, namátkou např.:
http://tma.main.jp/logic/index_en.html
https://leventozturk.com/engineering/karnaugh/
http://k-map.sourceforge.net/
Základem těchto programů je však minimalizace logické funkce pomocí algoritmu Quine-Mc Cluskey (viz navazující text), Karnaughova mapa pak slouží jen jako grafické zobrazení výsledku minimalizace.