Kapitola3
Převody forem funkcí pomocí Karnaughových map
Souhrn
V předešlém textu „Úvod do logických funkcí a logických obvodů“ jsme si vysvětlili v rámci kapitoly týkající se algebraického vyjádření logických funkcí, že rozlišujeme dva základní typy algebraického zápisu logické funkce – součtovou (disjunktní) a součinovou (konjunktní) formu funkce. Také jsme se přesvědčili, že každou logickou funkci můžeme vždy vyjádřit pomocí obou forem a to buď jako součet součinů (disjunktní forma), nebo jako součin součtů (konjunktní forma). V dané kapitole jsme si dále uvedli, že pro převod forem lze použít zákony Booleovy algebry a převod formy z disjunktní na konjunktní či naopak provést algebraicky. Tento způsob je však poměrně pracný a není navíc zaručeno, že převodem získáme opačnou formu v minimální podobě (záleží na pořadí aplikace zákonů a úprav). Proto si v této kapitole představíme způsob převodu forem funkce za pomoci Karnaughových map.
Definice
Při převodu forem, disjunktní na konjunktní a naopak, pomocí Karnaughovy mapy postupujeme v zásadě opačně, než při minimalizaci logické funkce. Ze zadané formy funkce vyplníme do mapy smyčky a příslušné funkční hodnoty, ze kterých daná forma původně vznikla, a ze zbývajících políček v mapě pomocí smyček pak získáme formu opačnou.
Při převodu forem funkcí neuvažujeme neurčité stavy, uvažujeme hodnoty funkce pouze logická 1 a logická 0. Ze zadaného algebraického tvaru (ať už disjunktního nebo konjunktního) totiž nelze poznat, zda daný výraz vznikl z nějakého neurčitého stavu nebo nikoliv.
3.1.1
Převod formy z disjunktní na konjunktní
Nejprve se podíváme na případ, kdy k funkci zadané pomocí disjunktní formy (součtová) máme nalézt její konjunktní (součinovou) formu.
Souhrn
Postup převodu z disjunktní na konjunktní formu dané funkce f můžeme shrnout:
  1. Postupně pro každý zadaný součinový term (implikant funkce) nalezneme v mapě smyčku z políček, ze kterých vznikl. Tato políčka se nacházejí v průsečíku oblastí pokrytých proměnnými obsaženými v daném implikantu. Z předchozího poznatku vyplývá, že počet políček této smyčky p odpovídá:
    p=2n-x ,
    kde p je počet políček hledané smyčky, n je počet všech nezávisle proměnných v mapě a x je počet nezávisle proměnných obsažených v daném implikantu.
  1. Do políček takto nalezené smyčky vepíšeme hodnotu logická 1 (neurčité stavy neuvažujeme, jak jsme si již vysvětlili výše). Postupně tímto způsobem do mapy vyplníme hodnotu logická 1 pro všechny zadané implikanty a jim odpovídající smyčky v mapě. Smyčky v mapě se mohou samozřejmě překrývat, proto pokud se na daném políčku již hodnota logická 1 nachází, další do ní nezapisujeme.
  1. Po vyplnění všech logických 1 do mapy na základě všech zadaných implikantů disjunktní formy vyplníme hodnotu logická 0 na všechna zbylá prázdná políčka v mapě.
  1. Dále postupujeme stejným způsobem, jako když hledáme MNKF formu funkce. Tzn., že vytvoříme smyčky z nulových bodů, zapíšeme jim odpovídající součinové termy, pokryjeme všechny nulové body v mapě a zapíšeme hledaný konjunktní tvar jako negaci logického součtu všech součinových termů pro jednotlivé smyčky.
  1. Tím získáme hledaný konjunktní tvar disjunktně zadané funkce f (pokud vytvoříme co nejmenší počet smyček z nulových bodů a tyto smyčky budou co největší, získáme přímo MNKF, jinak dostaneme obecný neminimální konjunktní tvar funkce f).
Vyzkoušejme uvedený postup na následujícím příkladu.
Příklad
Příklad:
Převeďte zadaný disjunktní tvar funkce f 4 nezávisle proměnných na konjunktní a určete přímo MNKF zadané funkce:
fD=a⋅b⋅c⋅d¯∨a⋅c¯⋅d¯∨b⋅d
Zobrazit řešení
Řešení
Řešení:
Budeme postupovat po jednotlivých krocích.
  1. Nakreslíme prázdnou Karnaughovu mapu 4 proměnných, viz obrázek 14.
+
14. Prázdná Karnaughova mapa pro 4 proměnné k řešení zadaného příkladu
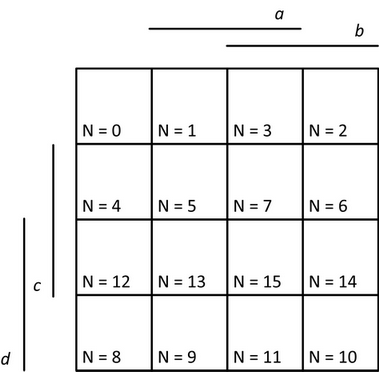
Obr. 14. Prázdná Karnaughova mapa pro 4 proměnné k řešení zadaného příkladu
  1. Postupně do mapy vyplníme logické 1 do políček odpovídajících smyčkám vzniklým z jednotlivých termů.
    1. Součinový term a⋅b⋅c⋅d¯ odpovídá smyčce vzniklé z jednoho políčka (1 = 24-4), které leží v průsečíku oblasti pokrytí – proměnnou a, proměnnou b, proměnnou c a mimo oblast pokrytí proměnnou d (proměnná d je negovaná). Tomu odpovídá políčko s indexem 7 (binárně vyjádřený index: 0111 = pořadí proměnných dcba).
    1. Další součinový term a⋅c¯⋅d¯ představuje smyčku ze dvou políček (1 = 24-3), která leží v průsečíku oblasti pokrytí proměnnou a a mimo oblasti pokrytí proměnnou c a proměnnou d. Tato dvě políčka mají tedy indexy: 1 (0001) a 3 (0011).
    1. Poslední součinový term b⋅d vznikl ze smyčky pokrývající 4 políčka v mapě (1 = 24-2) a tato 4 políčka leží v oblasti pokryté proměnnou b a proměnnou d. Čtveřice políček má tedy indexy: 10 (1010), 11 (1011), 14 (1110) a 15 (1111).
  1. Na zbylá prázdná políčka nyní doplníme hodnotu logická 0.
  1. Pokryjeme nulové body zadané funkce f v mapě pomocí smyček tak, abychom získali MNKF formu (postup stejný jako při minimalizaci a hledání MNKF). Výsledkem tak bude mapa s vyznačenými smyčkami na obrázku 15.
+
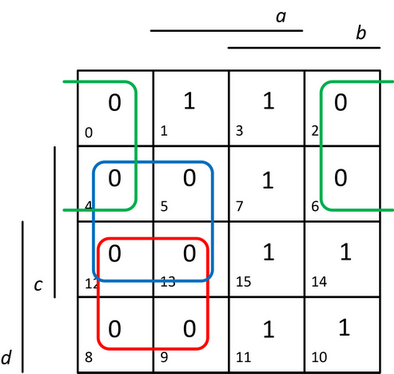
15. Karnaughova mapa s vyplněnými jednotkovými i nulovými body a vyznačenými smyčkami pro hledání MNKF
Obr. 15. Karnaughova mapa s vyplněnými jednotkovými i nulovými body a vyznačenými smyčkami pro hledání MNKF
  1. Nyní již jen standardně zapíšeme součinové vyjádření pro každou smyčku z nulových bodů a výslednou MNKF formu získáme jako negaci jejich logických součtů:
    fK=b¯⋅d∨b¯⋅c∨a¯⋅d¯¯=b∨d¯⋅b∨c¯⋅a∨d
Další příklad na převod formy funkce z disjunktní na konjunktní si zkusíme pro 5 nezávisle proměnných.
Příklad
Příklad:
Pro funkci f pěti nezávisle proměnných zadanou v disjunktním tvaru nalezněte její MNKF formu. Disjunktní forma funkce f je zadána:
fD=a⋅b¯⋅c⋅d∨a⋅b⋅c⋅d∨a⋅b¯⋅c¯∨a⋅d¯
Zobrazit řešení
Řešení
Řešení:
Pro funkci pěti proměnných nakreslíme její příslušnou mapu. Postupujeme pomocí stejných kroků, jako v příkladu výše, tedy pro každý zadaný součinový implikant nalezneme v mapě příslušnou smyčku a vyplníme ji logickými 1. Po vyplnění všech smyček (implikantů disjunktní formy v mapě) doplníme na zbývající políčka hodnoty logická 0, vyznačíme smyčky přes tyto nulové body a získáme výslednou MNKF. Postup řešení a výsledek zobrazuje následující animace 2.
Animace 2. Řešení příkladu určení MNKF funkce f pěti proměnných zadané v disjunktní formě
Konečné řešení vyplněné Karnaughovy mapy a určení MNKF zadané funkce f je uvedeno na obrázku 16.
+
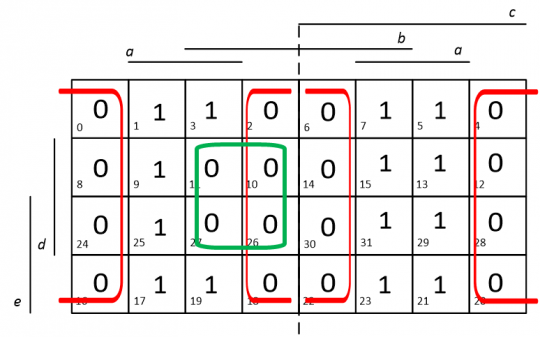
16. Výsledná Karnaughova mapa s vyplněnými jednotkovými i nulovými body a vyznačenými smyčkami pro hledání MNKF z příkladu
Obr. 16. Výsledná Karnaughova mapa s vyplněnými jednotkovými i nulovými body a vyznačenými smyčkami pro hledání MNKF z příkladu
Řešení MNKF zadané funkce je tedy:
fK=a¯∨b⋅c¯⋅d¯=a⋅b¯∨c∨d¯
3.1.2
Převod formy z konjunktní na disjunktní
Nyní se naopak zaměříme na druhý případ, kdy je úkolem k zadané konjunktní formě funkce nalézt její disjunktní formu.
Souhrn
Postup převodu z konjunktní na disjunktní formu dané funkce f je v zásadě značně obdobný, jako předchozí směr převodu, avšak s jedním podstatným rozdílem (viz dále). Jednotlivé kroky převodu tedy můžeme stručně popsat:
  1. Zadaný konjunktní tvar funkce f je potřeba nejprve znegovat. Upravíme výraz pomocí zákonů o negaci logického součtu a součinu. Tímto krokem získáme součinové implikanty představující smyčky vzniklé z nulových bodů funkce f.
  1. Další postup je v zásadě totožný jako v případě předchozího opačného směru převodu. Postupně opět pro každý zadaný součinový term nalezneme v mapě smyčku z políček, ze kterých vznikl. Políčka se nachází v průsečíku oblastí pokrytí jednotlivými proměnnými obsaženými v daném implikantu. Počet políček p opět odpovídá předchozí úvaze v závislosti na celkovém počtu proměnných v mapě (n) a na počtu proměnných obsažených v daném implikantu (x).
  1. Do políček takto nalezené smyčky vepíšeme hodnotu logická 0 (opět neuvažujeme neurčité stavy). Postupně vyplníme do mapy hodnotu logická 0 pro všechny zadané implikanty a jim odpovídající smyčky v mapě.
  1. Po vyplnění všech logických 0 do mapy na základě všech zadaných implikantů negace konjunktní formy vyplníme hodnotu logická 1 na všechna zbylá prázdná políčka v mapě.
  1. Dále postupujeme stejným způsobem, jako když hledáme MNDF formu funkce. Tzn., že vytvoříme smyčky z jednotkových bodů (pokryjeme všechny jednotkové body), zapíšeme jim odpovídající součinové termy a zapíšeme hledaný disjunktní tvar jako logický součet všech součinových termů pro jednotlivé smyčky.
  1. Tím získáme hledaný disjunktní tvar konjunktně zadané funkce f (opět můžeme získat rovnou MNDF formu funkce nebo jiný obecný neminimální disjunktní tvar funkce f).
Pro ověření správnosti postupu a pro jeho ilustraci uvedeme dva následující příklady.
Příklad
Příklad:
Zadaný konjunktní tvar funkce f čtyř proměnných převeďte na MNDF formu funkce f. Zadaný konjunktní tvar je následující:
fK=a∨b¯∨c⋅a∨b∨d⋅b∨c¯
Zobrazit řešení
Řešení
Řešení:
Budeme postupovat po jednotlivých krocích dle návodu uvedeného výše.
  1. Opět nakreslíme nejprve prázdnou Karnaughovu mapu 4 proměnných, viz obrázek 17.
+
17. Prázdná Karnaughova mapa pro 4 proměnné k řešení zadaného příkladu
Obr. 17. Prázdná Karnaughova mapa pro 4 proměnné k řešení zadaného příkladu
  1. Provedeme nyní negaci dané konjunktní formy a upravíme ji pomocí zákonů o negaci logického součtu a součinu. Tím získáme součinové termy (implikanty) pro smyčky v mapě vzniklé z nulových bodů funkce:
    fK¯=a∨b¯∨c⋅a∨b∨d⋅b∨c¯¯=a¯⋅b⋅c¯∨a¯⋅b¯⋅d¯∨b¯∨c
  1. Postupně do mapy vyplníme logické 0 do políček odpovídajících smyčkám vzniklým z jednotlivých termů.
    1. Součinový term a¯⋅b⋅c¯ odpovídá smyčce vzniklé ze dvou políček (1 = 24-3), které leží v průsečíku oblasti pokrytí proměnnou b a mimo oblast pokrytí proměnnými a, c. Tomu odpovídají políčka s indexy 2 (0010) a 10 (1010).
    1. Další součinový term a¯⋅b¯⋅d¯ představuje smyčku ze dvou políček (1 = 24-3), která leží v průsečíku – mimo oblasti pokrytí proměnnými a, b, d, což představuje políčka s indexy: 0 (0000) a 4 (0100).
    1. Poslední součinový term b¯∨c vznikl ze smyčky pokrývající 4 políčka v mapě (1 = 24-2) a tato 4 políčka leží v oblasti pokryté proměnnou c a mimo oblast pokrytí proměnnou b. Čtveřice políček má tedy indexy: 4 (0100), 5 (0101), 12 (1100) a 13 (1101).
  1. Na zbylá prázdná políčka nyní doplníme hodnotu logická 1.
  1. Pokryjeme jednotkové body zadané funkce f v mapě pomocí smyček tak, abychom získali MNDF formu, výslednou mapu se smyčkami ilustruje obrázek 18.
+
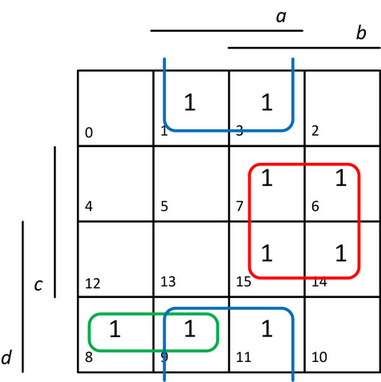
18. Řešení smyček z jednotkových bodů v mapě při převodu ze zadané konjunktní formy funkce do disjunktní formy (MNDF)
Obr. 18. Řešení smyček z jednotkových bodů v mapě při převodu ze zadané konjunktní formy funkce do disjunktní formy (MNDF)
  1. Zapíšeme nyní řešení MNDF formy funkce jako logický součet jednotlivých součinových termů:
    fD=b⋅c∨a⋅c¯∨b¯⋅c¯⋅d
Další příklad převodu z konjunktní formy funkce na disjunktní tvar si spočítáme pro 5 nezávisle proměnných.
Příklad
Příklad:
Zadanou konjunktní formu funkce f pěti proměnných převeďte pomocí Karnaughovy mapy na disjunktní formu, nalezněte MNDF formu funkce. Konjunktní forma funkce je dána:
fK=b¯∨c¯∨d∨e¯⋅b¯∨d∨e⋅b¯∨d∨e¯⋅a∨d¯
Zobrazit řešení
Řešení
Řešení:
Jedná se o funkci 5 proměnných, použijeme tedy Karnaughovu mapu s 32 políčky. Postup bude pak stejný jako v předchozím příkladu. Nejprve nakreslíme prázdnou Karnaughovu mapu pro 5 proměnných. Poté znegujeme zadanou konjunktní formu funkce, abychom získali disjunktní vyjádření pro nulové body funkce. Z těchto disjunktních termů vyplníme do mapy smyčky a v nich nulové body funkce. Do zbylých prázdných políček mapy vyplníme logické 1, vytvoříme smyčky z jednotkových bodů a získáme MNDF formu funkce.
Jednotlivé kroky a výsledné řešení představuje animace 3.
Animace 3. Řešení příkladu určení MNDF funkce f pěti proměnných zadané pomocí konjunktní formy
Konečné řešení vyplněné Karnaughovy mapy a určení MNKF zadané funkce f je uvedeno na obrázku 19.
+
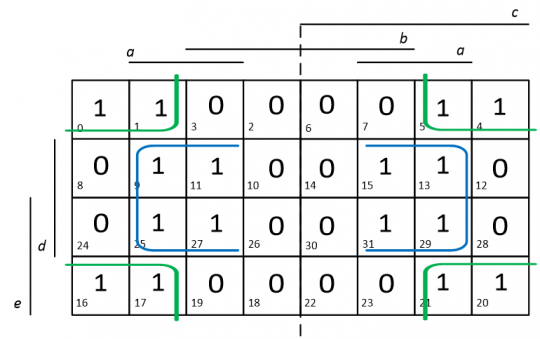
19. Řešení smyček v mapě pro nalezení MNDF formy z příkladu
Obr. 19. Řešení smyček v mapě pro nalezení MNDF formy z příkladu