Kombinační logické obvody a hazardy v kombinačních obvodech

2.2

Kodér a dekodér, převodníky kódů

Definice

Obecně lze kodér definovat jako kombinační logický obvod, který má n vstupů a m výstupů, kde maximální počet výstupů je dán:

m_{m a x} = \log_{2} n

. Na vstupu kodéru může být obecně pouze jeden z n vstupů aktivní (kód 1 z n) a kodér přiřadí tomuto jednomu aktivnímu vstupu danou kombinaci hodnot na m výstupech [5].

Dekodér je pak analogicky opačný kombinační obvod, který obsahuje n vstupů a m výstupů, kde maximální počet výstupů je dán:

m_{m a x} = 2^{n}

a z těchto m výstupů je v každý okamžik aktivní pouze jeden (kód 1 z n), který dekóduje vstupní kódovou posloupnost na n vstupech [5].

Poznámka

Zjednodušeně tedy kodér představuje obvod, který na výstupu „zakóduje“ vstupní kód do jiného, a dekodér naopak tento kód „dekóduje“ zpět na původní.

Kodéry a dekodéry tak velmi často plní v obvodech funkce převodníků kódů [5], ať už se jedná o převody mezi různými binárními kódy (např. z BCD kódu na jiný), převody mezi číselnými soustavami (z binární na osmičkovou, desítkovou apod.), nebo i převody kódů pro specifické aplikace a periferie (např. převod kódu pro segmentový displej) apod.

Pro ukázku jednoduchého kodéru a dekodéru si uvedeme příklad kodéru 4 na 2 a dekodéru 2 na 4. Kodér 4 na 2 má tedy čtyři datové vstupy, z nichž pouze jeden smí být v daný okamžik aktivní. Aby tato podmínka platila, musíme ji buď zajistit na jeho vstupech, nebo použít tzv. prioritní kodér. Jedná se o specifický případ kodéru, jehož vstupy mají nastavenu prioritu (obvykle ve směru vzestupném od jednoho vstupu k poslednímu v řadě), která zajistí, že stav vstupu s nejvyšší prioritou vždy převáží nad stavy vstupů s nižší prioritou (ty tak budou ignorovány). Proto je v následující zkrácené pravdivostní tabulce 6 tohoto kodéru použit vždy neurčitý stav, protože na stavech těchto vstupů v daném okamžiku nezáleží. V příkladu prioritního kodéru 4 na 2 v tabulce 6 a na obrázku 7 se vstupy a, b, c, d s prioritou vzestupně od vstupu a do d jsou výstupy kodéru označeny Q₀ a Q₁. Algebraické vyjádření výstupů je uvedeno níže pod tabulkou 6.

Tabulka 6. Pravdivostní tabulka jednoduchého prioritního kodéru 4 na 2.

d	c	b	a	Q₁	Q₀
0	0	0	1	0	0
0	0	1	X	0	1
0	1	X	X	1	0
1	X	X	X	1	1
0	0	0	0	X	X

Q_{0} = b \cdot \bar{c} \lor d

Q_{1} = c \lor d

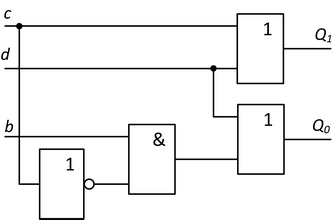
Obr. 7. Jednoduchý prioritní kodér 4 na 2.

Jako příklad jednoduchého dekodéru můžeme uvést přesně opačný dekodér 2 na 4. V tomto případě platí podmínka, že pouze jeden výstup Q smí být v daném okamžiku aktivní. Kombinacím možných stavů dvou datových vstupů dekodéru a, b odpovídá tedy pouze jeden aktivní výstup v jednom okamžiku z možných Q₀ až Q₃, jak ukazuje pravdivostní tabulka 7.

Tabulka 7. Pravdivostní tabulka jednoduchého dekodéru 2 na 4.

b	a	Q₃	Q₂	Q₁	Q₀
0	0	0	0	0	1
0	1	0	0	1	0
1	0	0	1	0	0
1	1	1	0	0	0

Pro jednotlivé výstupy vyjádříme jejich výstupní funkce:

Q_{0} = \bar{a} \cdot \bar{b}

Q_{1} = a \cdot \bar{b}

Q_{2} = \bar{a} \cdot b

Q_{3} = a \cdot b

A schéma zapojení tohoto dekodéru ukazuje obrázek 8.

Obr. 8. Jednoduchý dekodér 2 na 4.

Zajímavost

Pro zajímavost porovnejte realizaci a funkci tohoto jednoduchého dekodéru 2 na 4 na obrázku 8 a předchozího demultiplexoru 1 na 4 na obrázku 6. Tento dekodér v podstatě představuje daný demultiplexor pouze s tím rozdílem, že původní adresové vstupy demultiplexoru jsou v případě dekodéru realizovány přímo datovými vstupy a, b, a datový vstup x původního demultiplexoru tak chybí.

Zajímavost

Kodéry a dekodéry nalezneme rovněž mezi integrovanými obvody řady 7400 jako již hotové (de)kodéry určené pro různé aplikace, převody různých kódů, s různými počty vstupů a výstupů. Pro kodéry je častá realizace prioritního kodéru 10 na 4 nebo 8 na 3. Kodér 10 na 4 lze totiž využít pro převod čísel z desítkové (decimální) soustavy do dvojkové (binární), zatímco kodér 8 na 3 pro převod čísel z osmičkové (oktalové) do dvojkové (binární) soustavy. Kodér 10 na 4 lze nalézt v katalogu jako integrovaný obvod 74LS147, zatímco kodér 8 na 3 jako integrovaný obvod 74LS148.

Dekodéry mají mezi obvody řady 7400 větší zastoupení, např. integrovaný obvod 74LS137 představuje dekodér 3 na 8, 74LS139 obsahuje 2× v jednom pouzdře dekodér 2 na 4, 74LS145 je integrovaný dekodér (převodník) z BCD kódu do desítkové číselné soustavy a další. Samostatnou skupinu pak tvoří dekodéry pro zobrazení znaků (číslic) na segmentových displejích, např. 74LS247 a 74LS248 a další, které jsou k dispozici v různých úpravách (s tzv. otevřeným kolektorem, s pull-up rezistorem apod.)

Poznámka

Až dosud jsme ve všech textech operovali s binárními čísly v tzv. přímém dvojkovém kódu, tedy s přímou reprezentací (převodem) čísel mezi soustavami binární (dvojkovou) a decimální (desítkovou). Avšak kromě přímého převodu mezi číselnými soustavami lze pro vyjádření čísel ve dvojkové soustavě vytvořit i jiné binární kódy.

Definice

Kód představuje soubor pravidel pro jednoznačné vyjádření čísla v dané soustavě pomocí dostupných číslic.

Číslice představují symboly s určitou definovanou hodnotou v dané číselné soustavě.

V předchozím i následujícím textu uvažujeme pouze tzv. číselné soustavy polyadické, tedy takové soustavy, které jsou založeny na vyjádření čísla v dané soustavě pomocí jeho rozvoje v polynom a které mají základ číselné soustavy stejný na všech řádových místech (stupních polynomu). Tento základ soustavy je následně použit pro její pojmenování, mezi nejznámější patří soustavy: dvojková (binární), osmičková (oktalová), desítková (decimální), šestnáctková (hexadecimální).

Zajímavost

Kromě nich však existují i tzv. číselné soustavy nepolyadické, které nejsou založeny na polynomiálním rozvoji čísel, protože nemají stejný základ na všech řádových místech daného čísla. K těmto číselným soustavám patří např. tzv. číselné soustavy zbytkových tříd, jiným příkladem nepolyadické číselné soustavy jsou římská čísla.

Uveďme si v tabulce 6 pro ukázku převodní tabulky mezi BCD kódem a několika vybranými a v praxi častými binárními kódy.

Tabulka 6. Převodní tabulka vybraných binárních kódů.

N₍₁₀₎	BCD kód	Váhový 5421	Váhový 84-2-1	Grayův kód	F+3 kód	Kód 1 z n
0	0000	0000	0000	0000	0011	0000000001
1	0001	0001	0111	0001	0100	0000000010
2	0010	0010	0110	0011	0101	0000000100
3	0011	0011	0101	0010	0110	0000001000
4	0100	0100	0100	0110	0111	0000010000
5	0101	1000	1011	0111	1000	0000100000
6	0110	1001	1010	0101	1001	0001000000
7	0111	1010	1001	0100	1010	0010000000
8	1000	1011	1000	1100	1011	0100000000
9	1001	1100	1111	1101	1100	1000000000

BCD kód (Binary Coded Decimal) představuje přímý binární kód se čtyřmi řádovými pozicemi aplikovaný na každou jednotlivou číslici v desítkové soustavě, např. 27₍₁₀₎ = 0010 0111₍₂₎ v BCD kódu.

Váhové kódy využívají systém vah (koeficientů), kterými jsou násobeny (váhovány) jednotlivé řádové pozice. Některé kombinace vah umožňují vyjádřit všechny číslice 0–9 a některé mají rovněž své názvy v literatuře, např. 5421, 84-2-1 (Rubinoffův kód), 2421 a 3331 (Aikenovy kódy), aj.

Grayův kód je typ kódu se změnou na n řádech, konkrétně na jednom řádovém místě v případě dvou po sobě následujících číslech, a byl podrobně popsán v předchozích textech.

Kód F+3 (někdy též BCD+3, v angličtině Excess 3) je typ kódu s posunem, v tomto případě jsou všechny číslice v tomto kódu posunuty o tři oproti BCD kódu. Kód F+3 vykazuje symetričnost při vyjádření číslic vůči svému středu (např. 9 je negací 0, 8 je negací 1, atd.)

Kód 1 z n (v angličtině one-hot) je tzv. poziční kód, kdy číselné vyjádření určuje pozice číslice 1 v kódovém slově.

Definice

Převodníky kódů jsou dalšími často využívanými kombinačními logickými obvody v nejrůznějších situacích. Obvykle slouží k jednosměrnému převodu z jednoho binárního kódu do jiného, můžeme se ale setkat i s převodníky z jedné číselné soustavy do druhé (ty jsou nejčastěji realizovány pomocí dekodérů).

Převodníky kódů slouží k převodu kódů například při komunikaci různých periferií, převodu kódu na výstupu čítače či posuvného registru apod.

Jako ukázku jednoduchého převodníku si uveďme příklad realizace převodníku z BCD kódu do váhového kódu 5421, viz převodní tabulka 6 výše.

Příklad

Vyjdeme z uvedené převodní tabulky 6 a každému řádovému místu kódu 5421 přiřadíme vstupní proměnnou a, b, c, d a výstupy označíme Q₀, Q₁, Q₂ a Q₃. Obecně je zvykem v logických obvodech přiřadit proměnnou a (Q₀) na nejnižší řádové místo, tzv. LSB (Least Significant Bit), a v tomto případě proměnnou d (Q₃) na nejvyšší řádové místo, tzv. MSB (Most Significant Bit), čímž dostaneme převodní tabulku 7.

Tabulka 7. Převodní tabulka mezi BCD kódem a kódem 5421.

N₍₁₀₎	Kód 5421
N₍₁₀₎	Q₃ = d	Q₂ = c	Q₁ = b	Q₀ = a
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	1	0	0	0
6	1	0	0	1
7	1	0	1	0
8	1	0	1	1
9	1	1	0	0

Z ní můžeme jednoduše zapsat Karnaughovy mapy pro jednotlivé výstupní funkce Q₀, Q₁, Q₂ a Q₃, provést jejich minimalizace a získat např. minimální disjunktní formu pro každou výstupní funkci. Vzhledem k tomu, že v kódu uvažujeme pouze číslice 0–9, budou v políčkách Karnaughovy mapy pro indexy 10–15 neurčité stavy X, které můžeme využít při minimalizaci, jak ukazuje obrázek 9.

Obr. 9. Karnaughovy mapy pro vyjádření a minimalizaci jednotlivých výstupních funkcí převodníku.

Díky tomu můžeme vyjádřit minimální disjunktní tvary jednotlivých funkcí a upravit je pro realizaci pomocí hradel NAND:

Q_{0} = \bar{a} \cdot d \lor a \cdot \bar{c} \cdot \bar{d} \lor \bar{a} \cdot b \cdot c = \bar{\bar{\bar{a} \cdot d} \cdot \bar{a \cdot \bar{c} \cdot \bar{d}} \cdot \bar{\bar{a} \cdot b \cdot c}}

Q_{1} = a \cdot b \lor \bar{a} \cdot d \lor b \cdot \bar{c} = \bar{\bar{a \cdot b} \cdot \bar{\bar{a} \cdot d} \cdot \bar{b \cdot \bar{c}}}

Q_{2} = a \cdot d \lor \bar{a} \cdot \bar{b} \cdot c = \bar{\bar{a \cdot d} \cdot \bar{\bar{a} \cdot \bar{b} \cdot c}}

Q_{3} = d \lor a \cdot c \lor b \cdot c = \bar{\bar{d} \cdot \bar{a \cdot c} \cdot \bar{b \cdot c}}

Konečnou realizaci převodníku pomocí hradel NAND představuje obrázek 10.

Obr. 10. Zapojení převodníku z kódu BCD do kódu 5421 pomocí hradel NAND.