Elektrotechnika II

4.2

Elektrické (elektrostatické) vlastnosti

4.2.1

Náhradní zapojení kondenzátoru

4.2.1.1

Ideální kondenzátor

Pojem ideální kondenzátor označuje součástku, která má pouze vlastní kapacitu. Náhradní obvod (model) ideálního kondenzátoru má následující podobu:

Obr. 30. Ideální kondenzátor, fázorový diagram

Základní vlastnosti ideálního kondenzátoru jsou následující:

Jediným charakteristickým parametrem je hodnota kapacity.

Kondenzátor nevykazuje žádný tzv. parazitní odpor ani indukčnost, odpor dielektrika je nekonečně velký.

Připojením ideálního kondenzátoru paralelně ke svorkám ideálního zdroje konstantního napětí se kondenzátor nabije (akumuluje náboj) za nulový čas (ihned).

Při zvyšování napětí na kondenzátoru (nabíjecí proces) se hodnota proudu procházející kondenzátorem snižuje (fázový posun φ mezi proudem a napětím je 90º).

V obvodu střídavého (harmonického) napětí je fázový posun mezi proudem a napětím 90º.

V obvodu střídavého napětí se kondenzátor chová jako odpor o velikosti X_C (kapacitní reaktance).

Základní charakteristikou kondenzátorů, která popisuje závislost základních fyzikálních veličin, je tzv. voltcoulombová charakteristika:

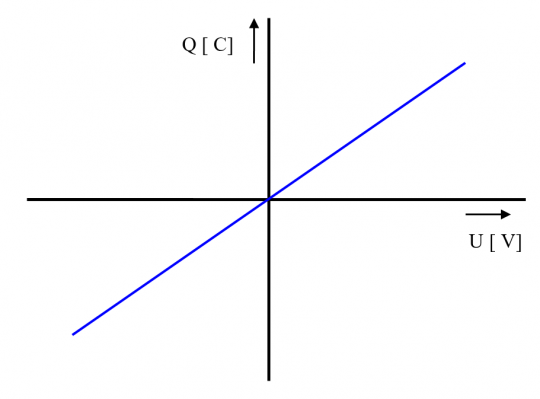
Obr. 31. Voltcoulombová charakteristika kondenzátoru

Tato charakteristika popisuje vztah mezi kapacitou, nábojem a napětím na kondenzátoru. Vztah těchto tří parametrů můžeme zapsat:

Q = C \cdot U_{C} [C; F, V]

kde Q je náboj uložený na deskách kondenzátoru, C je kapacita kondenzátoru a U_C je napětí na deskách kondenzátoru.

Definice

Velikost náboje uloženého na deskách kondenzátoru je přímo úměrná velikosti kapacity kondenzátoru a velikosti přiloženého napětí.

4.2.1.2

Skutečný kondenzátor

Skutečný kondenzátor má na rozdíl od ideálního kondenzátoru další parametry, které se mohou v obvodových aplikacích projevit. Skutečný kondenzátor popisujeme následujícími parametry:

kapacita (základní vlastnost ideálního kondenzátoru),

ztrátový odpor (paralelní R_P nebo sériový R_S).

Do hodnoty ztrátového odporu zahrnujeme veškeré ztráty, které v kondenzátoru vznikají. Míru výkonových ztrát vyjadřuje ztrátový činitel tg δ (čti: tangens delta). Výkonové ztráty vznikají:

odporem přívodních vodičů a proudovým odporem dielektrika,

polarizací dielektrika,

hysterezí dielektrika,

vyzařováním.

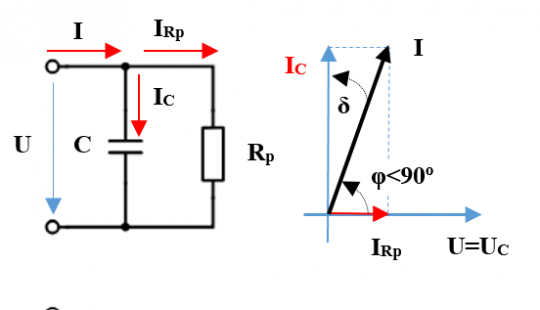
Obr. 32. Náhradní zapojení skutečného kondenzátoru

Náhradní zapojení vychází z paralelního zapojení ideálního kondenzátoru C a ztrátového odporu R_P. V tomto zapojení platí pro ztrátový činitel tg δ:

t g δ = \frac{I_{R P}}{I_{C}} = \frac{1}{ω \cdot R_{P} \cdot C} \cdot

Ztrátový činitel tg δ, který charakterizuje jakost dielektrika, bývá u kondenzátorů 10^-1 až 10^-6.

4.2.2

Intenzita elektrického pole

Značí se symbolem E a jednotkou je [V·m^-1]. Výpočet je definován vztahem:

E = \frac{U}{l} [V \cdot m^{- 1}; V, m],

kde E je intenzita elektrického pole kondenzátoru, U je napětí mezi deskami kondenzátoru, l je vzdálenost desek kondenzátoru.

Velikost intenzity elektrického pole rozhoduje o nebezpečí průrazu izolující vrstvy mezi vodivými deskami kondenzátoru (dielektrika). Základní dielektrické materiály kondenzátorů se vyznačují těmito hodnotami průrazné pevnosti E [kV/mm]:

vzduch E = 2,14,

keramika E = 20–40,

slída E = 40,

kondenzátorový papír E = 10–20,

polystyren E = 50.

4.2.3

Dielektrikum

Dielektrikum je označení pro speciální izolant, který tvoří prostředí mezi deskami kondenzátoru. Vložením dielektrika dojde ke zvýšení kapacity kondenzátoru. Připojením kondenzátoru ke zdroji napětí dochází k tzv. polarizaci dielektrika. Základní vlastností dielektrika je relativní permitivita Ɛ_r. Je to bezrozměrná konstanta (pro daný materiál dielektrika), která udává, kolikrát je permitivita dielektrického materiálu větší než permitivita vakua.

4.2.4

Charakteristika

V předchozích kapitolách jsme hovořili o odporových prvcích. Jejich charakteristickými veličinami bylo napětí a proud a charakteristika se nazývala voltampérová. U kondenzátoru je charakteristickou veličinou napětí a náboj.

4.2.5

Energie akumulovaná v kondenzátoru

Po nabití je na deskách kondenzátoru uložený náboj, který je nositelem energie. Velikost energie akumulovaná v kondenzátoru je definována:

W = \frac{1}{2} \cdot Q \cdot U [J; C, V],

kde W je energie elektrostatického pole [Ws = J (joul)], Q je náboj uložený v kondenzátoru [C], U je napětí na svorkách kondenzátoru [V].

Základní vztah můžeme upravit:

W = \frac{1}{2} \cdot Q \cdot U = \frac{1}{2} \cdot C \cdot U \cdot U = \frac{1}{2} \cdot C \cdot U^{2} [J; F, V] .

Energie uložená v kondenzátoru je uchována dlouhodobě, ubývá jí pouze tzv. samovybíjením kondenzátoru (nedokonalá izolace dielektrika).