Elektrotechnika IV

4.3

Filtry typu dolní propust

Filtr typu dolní propust můžeme realizovat pomocí rezistoru a kondenzátoru nebo cívky a rezistoru.

4.3.1

Filtr typu dolní propust realizovaný rezistorem a kondenzátorem

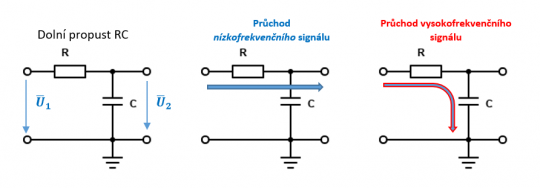
Obr. 36. Zapojení filtru RC (dolní propust)

Přenosovou funkci odvodíme:

\bar{A_{U}} = \frac{\bar{Z_{2}}}{\bar{Z_{1}} + \bar{Z_{2}}} \bar{Z_{2}} j e i m p e d a n c e k o n d e n z á t o r u C, \bar{Z_{1}} j e i m p e d a n c e r e z i s t o r u R

\bar{A_{U}} = \frac{\frac{1}{j ω \cdot C}}{R + \frac{1}{j ω \cdot C}} = \frac{\frac{1}{j ω \cdot C}}{\frac{j ω \cdot R \cdot C + 1}{j ω \cdot C}} = \frac{1}{1 + j ω \cdot R \cdot C} v y n á s o b í m e k o m p l e x n ě s d r u ž e n ý m č í s l e m

\bar{A_{U}} = \frac{1}{1 + j ω \cdot R \cdot C} \cdot \frac{1 - j ω \cdot R \cdot C}{1 - j ω \cdot R \cdot C} = \frac{1 - j ω \cdot R \cdot C}{1^{2} - j ω \cdot R \cdot C + j ω \cdot R \cdot C - j^{2} \cdot ω^{2} \cdot R^{2} \cdot C^{2}}

Upravíme výraz s imaginární jednotkou

j^{2} = - 1

a dostaneme:

\bar{A_{U}} = \frac{1 - j ω \cdot R \cdot C}{1 + ω^{2} \cdot R^{2} \cdot C^{2}} v ý r a z r o z d ě l í m e n a r e á l n o u a i m a g i n á r n í č á s t

\bar{A_{U}} = r e á l n á - j \cdot i m a g i n á r n í = \frac{1}{1 + ω^{2} \cdot R^{2} \cdot C^{2}} - j \cdot \frac{ω \cdot R \cdot C}{1 + ω^{2} \cdot R^{2} \cdot C^{2}}

Velikost přenosu (modul přenosu)

|\bar{A_{U}}|

vyjádříme:

|\bar{A_{U}}| = f (f) = \sqrt{{(\frac{1}{1 + ω^{2} \cdot R^{2} \cdot C^{2}})}^{2} + \frac{ω^{2} \cdot R^{2} \cdot C^{2}}{{(1 + ω^{2} \cdot R^{2} \cdot C^{2})}^{2}}} = \sqrt{\frac{1}{1 + ω^{2} \cdot R^{2} \cdot C^{2}}}

|\bar{A_{U}}| = \frac{1}{\sqrt{1 + ω^{2} \cdot R^{2} \cdot C^{2}}}

Pro fázový posun napětí

φ_{U}

odvodíme:

φ_{U} = a r c t g \frac{i m a g i n á r n í č á s t \bar{A_{U}}}{r e á l n á č á s t \bar{A_{U}}} = \frac{- \frac{ω \cdot R \cdot C}{1 + ω^{2} \cdot R^{2} \cdot C^{2}}}{\frac{1}{1 + ω^{2} \cdot R^{2} \cdot C^{2}}}

φ_{U} = a r c t g (- ω \cdot R \cdot C) = - a r c t g (ω \cdot R \cdot C)

Obr. 37. [Příklad č. 30] Filtr RC (dolní propust) – amplitudová frekvenční charakteristika

Příklad

[Příklad č. 30] Nakreslete amplitudovou frekvenční charakteristiku filtru typu dolní propust s rezistorem R a kondenzátorem C.

Zobrazit řešení

Skrýt řešení

Řešení

Jednotlivé body charakteristiky

|A_{U}| = f (f)

získáme dosazením do vzorce:

|\bar{A_{U}}| = \sqrt{\frac{1}{1 + ω^{2} \cdot R^{2} \cdot C^{2}}}, v ý r a z ω j e d e f i n o v a n ý : ω = 2 \cdot π \cdot f

Mezní kmitočet filtru je definován vztahem:

f_{m} = \frac{1}{2 π \cdot R \cdot C}

Pro

ω = 0

získáme hodnotu

|A_{U}|

|\bar{A_{U}}| = \sqrt{\frac{1}{1 + 0^{2} \cdot R^{2} \cdot C^{2}}} = \sqrt{\frac{1}{1 + 0}} = \sqrt{\frac{1}{1}} = \sqrt{1} = 1

a_{U} = 20 \cdot l o g |\bar{A_{U}}| = 20 \cdot \log 1 = 20 \cdot 0 = 0 d B .

Pro

ω = \infty

získáme hodnotu

|A_{U}|

|\bar{A_{U}}| = \sqrt{\frac{1}{1 + \infty^{2} \cdot R^{2} \cdot C^{2}}} = \sqrt{\frac{1}{\infty^{2}}} = \frac{1}{\infty} = 0

Pro

ω = ω_{m} = \frac{1}{R C}

(mezní kmitočet f_M) získáme hodnotu

|A_{U}|

|\bar{A_{U}}| = \sqrt{\frac{1}{1 + \frac{1}{R^{2} \cdot C^{2}} \cdot R^{2} \cdot C^{2}}} = \sqrt{\frac{1}{1 + 1}} = \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} = 0,707 [-]

a_{U} = 20 \cdot l o g |\bar{A_{U}}| = 20 \cdot \log 0,707 = 20 \cdot (- 0,1506) ≐ - 3 d B .

Obr. 38. [Příklad č. 31] Filtr RC (dolní propust) – fázová frekvenční charakteristika

Příklad

[Příklad č. 31] Nakreslete fázovou frekvenční charakteristiku filtru typu dolní propust s rezistorem R a kondenzátorem C.

Zobrazit řešení

Skrýt řešení

Řešení

Jednotlivé body charakteristiky

φ_{U} = f (f)

získáme dosazením do vztahu:

φ_{U} = a r c t g (- ω \cdot R \cdot C) = - a r c t g (ω \cdot R \cdot C)

Pro

ω = 0

získáme hodnotu

φ_{U} :

φ_{U} = - a r c t g (ω \cdot R \cdot C) = - a r c t g (0 \cdot R \cdot C) = - a r c t g (0) = 0 ° .

Pro

ω = \infty

získáme hodnotu

φ_{U} :

φ_{U} = - a r c t g (\infty \cdot R \cdot C) = - a r c t g (\infty) = - 90 ° .

Pro

ω = \frac{1}{R C}

získáme hodnotu

φ_{U} :

φ_{U} = - a r c t g (\frac{1}{R \cdot C} \cdot R \cdot C) = - a r c t g (1) = - 45 ° .

4.3.2

Filtr typu dolní propust realizovaný rezistorem a cívkou

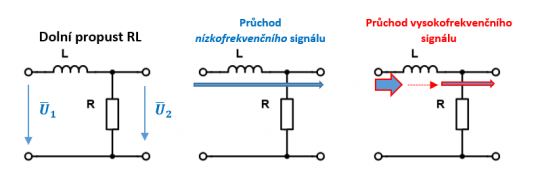
Obr. 39. Zapojení filtru RL (dolní propust)

Přenosovou funkci odvodíme:

\bar{A_{U}} = \frac{\bar{Z_{2}}}{\bar{Z_{1}} + \bar{Z_{2}}} \bar{Z_{2}} j e i m p e d a n c e r e z i s t o r u R, \bar{Z_{1}} j e i m p e d a n c e c í v k y L

\bar{A_{U}} = \frac{R}{j ω \cdot L + R} č i t a t e l i j m e n o v a t e l r o z š í ř í m e v ý r a z e m \frac{1}{R}

\bar{A_{U}} = \frac{\frac{R}{R}}{j ω \cdot \frac{L}{R} + \frac{R}{R}} = \frac{1}{1 + j ω \frac{L}{R}} v y n á s o b í m e k o m p l e x n ě s d r u ž e n ý m č í s l e m

\bar{A_{U}} = \frac{1}{1 + j ω \cdot \frac{L}{R}} \cdot \frac{1 - j ω \cdot \frac{L}{R}}{1 - j ω \cdot \frac{L}{R}} = \frac{1 - j ω \cdot \frac{L}{R}}{1^{2} - j ω \frac{L}{R} + j ω \cdot \frac{L}{R} - j^{2} ω^{2} \cdot {(\frac{L}{R})}^{2}}

Upravíme výraz s imaginární jednotkou

j^{2} = - 1

a dostaneme:

\bar{A_{U}} = \frac{1 - j ω \cdot \frac{L}{R}}{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}} v ý r a z r o z d ě l í m e n a r e á l n o u a i m a g i n á r n í č á s t

\bar{A_{U}} = r e á l n á - j \cdot i m a g i n á r n í = \frac{1}{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}} - j \cdot \frac{ω \cdot \frac{L}{R}}{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}}

Velikost přenosu (modul přenosu)

|\bar{A_{U}}|

vyjádříme:

|\bar{A_{U}}| = f (f) = \sqrt{{(\frac{1}{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}})}^{2} + {(\frac{ω \cdot \frac{L}{R}}{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}})}^{2}}

|\bar{A_{U}}| = \sqrt{\frac{1}{{(1 + ω^{2} \cdot {(\frac{L}{R})}^{2})}^{2}} + \frac{ω^{2} \cdot {(\frac{L}{R})}^{2}}{{(1 + ω^{2} \cdot {(\frac{L}{R})}^{2})}^{2}}} = \sqrt{\frac{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}}{{(1 + ω^{2} \cdot {(\frac{L}{R})}^{2})}^{2}}}

|\bar{A_{U}}| = \sqrt{\frac{1}{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}}}

|\bar{A_{U}}| = \frac{1}{\sqrt{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}}}

Pro fázový posun odvodíme:

φ_{U} = a r c t g \frac{i m a g i n á r n í č á s t \bar{A_{U}}}{r e á l n á č á s t \bar{A_{U}}} = \frac{- \frac{ω \cdot \frac{L}{R}}{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}}}{\frac{1}{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}}}

φ_{U} = a r c t g (- ω \cdot \frac{L}{R}) = - a r c t g (ω \cdot \frac{L}{R}) = - a r c t g (\frac{ω \cdot L}{R})

Obr. 40. [Příklad č. 32] Filtr RL (dolní propust) – frekvenční přenosová charakteristika

Příklad

[Příklad č. 32] Nakreslete frekvenční přenosovou charakteristiku filtru typu dolní propust s rezistorem a cívkou.

Zobrazit řešení

Skrýt řešení

Řešení

Jednotlivé body charakteristiky

|A_{U}| = f (f)

získáme dosazením do vztahu:

|\bar{A_{U}}| = \frac{1}{\sqrt{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}}}, v ý r a z ω j e d e f i n o v a n ý : ω = 2 \cdot π \cdot f

Pro

ω = 0

získáme hodnotu

|A_{U}|

|\bar{A_{U}}| = \frac{1}{\sqrt{1 + ω^{2} \cdot {(\frac{L}{R})}^{2}}} = \frac{1}{\sqrt{1 + 0^{2} \cdot {(\frac{L}{R})}^{2}}} = \frac{1}{\sqrt{1 + 0}} = \frac{1}{\sqrt{1}} = 1

a_{U} = 20 \cdot l o g |\bar{A_{U}}| = 20 \cdot \log 1 = 20 \cdot 0 = 0 d B

Pro

ω = \infty

získáme hodnotu

|A_{U}|

|\bar{A_{U}}| = \frac{1}{\sqrt{1 + \infty \cdot {(\frac{L}{R})}^{2}}} = \frac{1}{\sqrt{1 + \infty}} = \frac{1}{\infty} = 0

Pro

ω_{m} = \frac{R}{L}

získáme hodnotu

|A_{U}|

|\bar{A_{U}}| = \frac{1}{\sqrt{1 + {(\frac{R}{L})}^{2} \cdot {(\frac{L}{R})}^{2}}} = \frac{1}{\sqrt{1 + 1}} = \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{1}} = 0,707

a_{U} = 20 \cdot l o g |\bar{A_{U}}| = 20 \cdot \log 0,707 = 20 \cdot 0 = - 3 d B

Obr. 41. [Příklad č. 33] Filtr RL (dolní propust) – frekvenční fázová charakteristika

Příklad

[Příklad č. 33] Nakreslete fázovou frekvenční charakteristiku filtru typu dolní propust s rezistorem a kondenzátorem.

Zobrazit řešení

Skrýt řešení

Řešení

Jednotlivé body charakteristiky

φ_{U} = f (f)

získáme dosazením do vztahu:

φ_{U} = - a r c t g (\frac{ω \cdot L}{R})

Pro

ω = 0

získáme hodnotu

φ_{U} :

φ_{U} = - a r c t g (\frac{0 \cdot L}{R}) = - a r c t g (0) = 0 ° .

Pro

ω = \infty

získáme hodnotu

φ_{U} :

φ_{U} = - a r c t g (\frac{\infty \cdot L}{R}) = - a r c t g (\infty) = - 90 ° .

Pro

ω_{m} = \frac{R}{L}

získáme hodnotu

φ_{U} :

φ_{U} = - a r c t g (\frac{\frac{R}{L} \cdot L}{R}) = - a r c t g (1) = - 45 ° .