Periodický neharmonický ustálený stav (PNUS)

Kapitola4

Výkon neharmonického napětí a proudu

Jestliže zdroj periodického napětí u(t) dodává do obvodu proud i(t), je okamžitá hodnota výkonu

p = u . i [W]

Činný výkon je střední hodnota tohoto výkonu v době jedné periody, tj.

P = \frac{1}{T} \int_{0}^{T} u . i d t [W]

Časové průběhy napětí a proudu vyjádříme ve tvaru Fourierových řad:

u (t) = U_{0} + \sum_{k = 1}^{\infty} U_{m k} . s i n (k ω_{0} t + θ_{k})

i (t) = I_{0} + \sum_{k = 1}^{\infty} I_{m k} . s i n (k ω_{0} t + ϑ_{k})

Celkový činný výkon je superpozicí činných výkonů jednotlivých harmonických a výkonu stejnosměrné složky, tj.:

P = U_{0} I_{0} + \sum_{k = 1}^{\infty} \frac{U_{m k} . I_{m k}}{2} . c o s (θ_{k} - ϑ_{k})

Zavedeme-li do tohoto vztahu efektivní hodnoty jednotlivých harmonických a vzájemný posun k-té harmonické, napětí a proudu

φ_{k} = θ_{k} - ϑ_{k}

, dostaneme:

Definice

P = U_{0} I_{0} + \sum_{k = 1}^{\infty} U_{k} I_{k} . c o s φ_{k}

Poznámka

Z celého popisu vyplývá, že harmonické složky o nestejných kmitočtech spolu nedávají žádný činný výkon

Pro definici jalového výkonu akceptujeme dohodu o smyslu fázového posunu harmonických napětí a proudů

φ_{k}

Stejně jako u harmonických veličin budeme předpokládat, že se jedná pro každou harmonickou o úhel měřený od složky proudu ke složce napětí.

Jalový výkon pak definujeme vztahem:

Definice

Q = \sum_{k = 1}^{\infty} U_{k} I_{k} . s i n φ_{k}

Důležitější je zdánlivý výkon, protože je vhodnou veličinou k posouzení míry využití zdrojů.

Definujeme jej jako součin efektivní hodnoty napětí a proudu.

Definice

S = U . I

Poměr činného a zdánlivého výkonu je účiník λ=cos φ.

λ = \frac{P}{S} = \cos φ

Mezi zdánlivým, činným a jalovým výkonem zde obecně platí vztah:

S^{2} \geq P^{2} + Q^{2}

Obvykle jej píšeme ve tvaru

S^{2} = P^{2} + Q^{2} + D^{2}

kde D je tzv. deformační výkon.

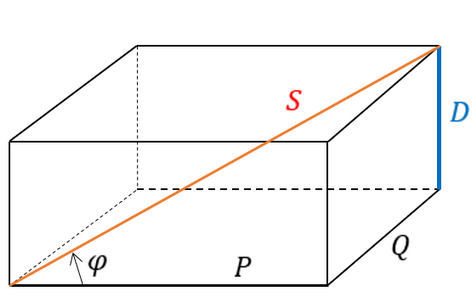
Obr. 8. Deformační výkon D