Projekce klasické filmové kopie (filmová optika + filmová kopie)

1.1

Maxwellova elektromagnetická teorie

Světlo je viditelná část elektromagnetického vlnění. Z Maxwellových rovnic plyne, že rychlost světla v elektricky nevodivém prostředí se vypočte dle vztahu (1):

v = \frac{1}{\sqrt{{ε_{0} ε}_{r} {μ_{0} μ}_{r}}}

kde

ε_{0}

je permitivita vakua,

ε_{r}

je relativní permitivita prostředí,

μ_{0}

je permeabilita vakua a

μ_{r}

je relativní permeabilita prostředí.

Ve vakuu mají relativní permitivita a relativní permeabilita hodnotu rovnou jedné. Rychlost světla ve vakuu je pak dána vztahem (2):

c = \frac{1}{\sqrt{ε_{0} μ_{0}}}

Dosazením permitivity a permeability vakua do vzorce (1) vyjde rychlost světla ve vakuu

c

, která je přibližně

3 \cdot 10^{8} m \cdot s^{- 1}

. Rychlost světla ve vakuu nezávisí na kmitočtu. V hmotných prostředích, kde platí, že

v < c

, je rychlost světla závislá na hustotě prostředí (reprezentovanou indexem lomu n, diskutováno dále v kapitole 1.3) a na kmitočtu f. Při průchodu bílého světla rozhraním dvou prostředí tak díky rozdílným indexům lomu vzniká disperze (rozptyl) světla.

Vlnová délka (délka jedné periody kmitání) se vypočte dle vztahu (3):

λ = \frac{v}{f}

kde

v

je rychlost světla a

f

je kmitočet.

Zajímavost

Změny elektrické a magnetické složky jsou spolu pevně svázány a popisují je tzv. Maxwellovy rovnice. Ze zobecněného Ampérova zákona vychází skutečnost, že časové a prostorové změny magnetické složky elektromagnetického pole jsou vázány s časovými změnami elektrické složky elektromagnetického pole. Z Faradayova indukčního zákona vychází skutečnost, že časové a prostorové změny elektrické složky elektromagnetického pole jsou vázány s časovými změnami magnetické složky elektromagnetického pole. Obě dvě složky jsou navzájem kolmé. Vektorovým součinem těchto vektorů dostáváme třetí, tzv. Poyntingův vektor, který je rovněž kolmý na oba vektory. Jde o směrový vektor udávající směr šíření výkonu vlny. Pro jednotlivé elektromagnetické vlny platí jejich vzájemná nezávislost.

Definice

Elektromagnetická vlna je složena ze tří navzájem kolmých (lineárně nezávislých) vektorů:

vektor intenzity elektrického pole $\vec{E}$

vektor magnetické indukce $\vec{B}$

směrový vektor $\vec{k}$

Elektromagnetická vlna je znázorněna na obr. 1.

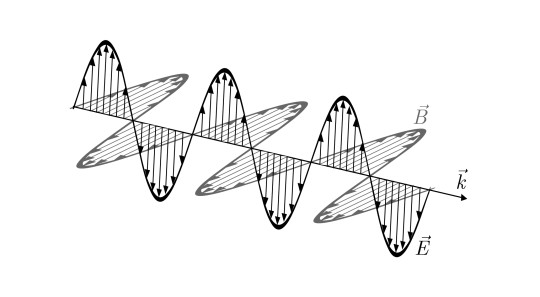
Obr. 1. Elektromagnetická vlna